問題
点(ノード)と道路候補(エッジ)からなるグラフにおいて、
エッジ上に道路を設置することを考える。
いくつかのノード間で移動ができるようにしたい。
移動したいノードの組の集合を需要とよぶ。
需要を満たす総移動距離を利便性とする。
設置費用と利便性を最適化せよ。
組合せ最適化を使うとこのような問題も解くことができます。
考え方
設置費用だけであれば、典型問題の中の最小全域木問題またはシュタイナー木問題になります。
利便性だけであれば、典型問題の最小費用流問題の変種である多品種最小費用流問題となります。
設置費用を下げると利便性が悪くなり、利便性を上げると設置費用が悪くなります。
このように複数の評価尺度がある最適化問題を多目的最適化問題とよびます。
ここでは、設置費用と利便性のトレードオフを求めてみましょう。
そのためには、設置費用に上限をつけながら、多品種最小費用流問題ベースの数理問題を何回も解くことにします。
定式化
| $\mbox{objective}$ | $\sum_i{\sum_j{\sum_k{x_{ijk}}}}$ | 利便性 |
| $\mbox{variables}$ | $x_{ijk} \ge 0 ~ \forall i, j, k$ | 需要iに対するノードjからノードjへの流量 |
| $y_{jk} \in \{0, 1\} ~ \forall j, k$ | ノードjとノードk間に道路を設置するかどうか | |
| $\mbox{subject to}$ | $\sum_{j,k}{y_{jk}} \le 上限$ | 設置費用上限 |
| $x_{ijk} \le y_{jk} ~ \forall i, j, k$ | xの制約 | |
| $\sum_k{x_{ijk}} = \sum_k{x_{ikj}} + 需要 ~ \forall i, j$ | 流量保存 |
Pythonで解く
必要なものを準備します。
python
import random, numpy as np, pandas as pd, networkx as nx
import matplotlib.pyplot as plt
from itertools import chain, combinations
from pulp import (LpBinary, LpProblem, LpVariable,
lpDot, lpSum, value)
def draw(g):
"""描画"""
nx.draw_networkx_labels(g, pos=pos)
nx.draw_networkx_nodes(g, node_color='w', pos=pos)
nx.draw_networkx_edges(g, pos=pos)
plt.show()
def addvar(cnt=[0], *args, **kwargs):
"""変数作成"""
cnt[0] += 1
return LpVariable('v%d'%cnt[0], lowBound=0, *args, **kwargs)
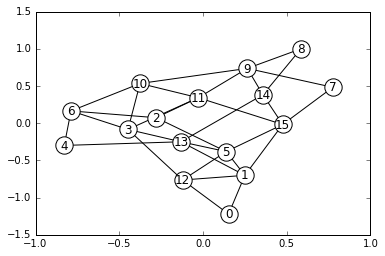
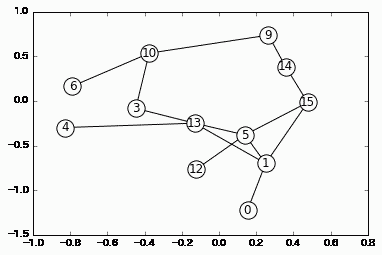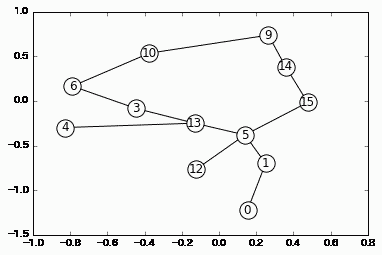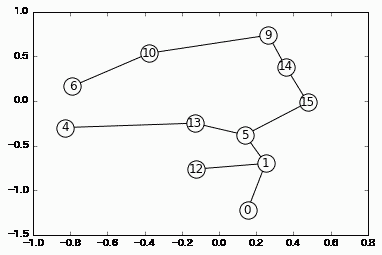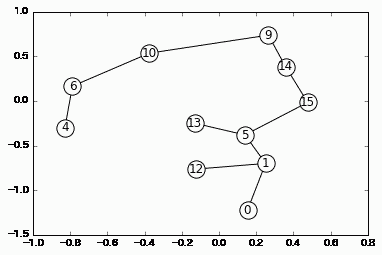
ランダムに問題を作ってみましょう。需要は一部のノード間のみに設定しました。
python
n = 16 # ノード数
g = nx.random_graphs.fast_gnp_random_graph(n, 0.26, 8) # グラフ
rn = g.nodes() # ノードリスト
pos = nx.spring_layout(g, pos={i:(i/4, i%4) for i in rn}) # ノード位置
for i, j in g.edges:
v = pos[i] - pos[j]
g[i][j]['dist'] = np.sqrt(v.dot(v)) # 距離
dems = random.sample(list(combinations(rn, 2)), 10) # 需要
draw(g)
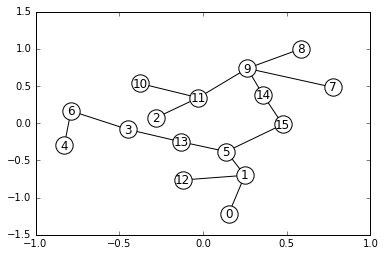
試しに最小全域木を求めてみます。
python
h = nx.minimum_spanning_tree(g, 'dist')
draw(h)
解いてみます。
python
rved = [(j, i) for i, j in g.edges] # 逆向きの辺
# 需要ごとの流量
a = pd.DataFrame([(df, dt, ef, et, g.edges[ef, et]['dist'], addvar())
for df, dt in dems for ef, et in chain(g.edges, rved)],
columns=['DeFr', 'DeTo', 'EdFr', 'EdTo', 'Dist', 'Var'])
# 辺を設置するかどうか
b = pd.DataFrame([(fr, to, g.edges[fr, to]['dist'], addvar(cat=LpBinary))
for fr, to in g.edges], columns=['Fr', 'To', 'Dist', 'Var'])
res = [] # 解(設置費用, 利便性, グラフ)
mxcst = 999 # 設置費用上限
while True:
m = LpProblem() # 数理モデル
m += lpDot(a.Dist, a.Var) + lpDot(b.Dist, b.Var)*1e-6 # 目的関数(利便性)
m += lpDot(b.Dist, b.Var) <= mxcst # 設置費用上限
for _, r in a.iterrows():
i, j = r.EdFr, r.EdTo
if i > j: i, j = j, i
# 流量を流す場合は、設置する
m += r.Var <= lpSum(b.query('Fr==%s & To==%s'%(i,j)).Var)
for (df, dt), c in a.groupby(['DeFr', 'DeTo']):
for nd in rn:
z = 1 if nd == df else -1 if nd == dt else 0
# 流量保存
m += lpSum(c.query('EdFr == %s'%nd).Var) == \
lpSum(c.query('EdTo == %s'%nd).Var) + z
m.solve() # 求解
if m.status != 1: break
a['Val'] = a.Var.apply(lambda v: value(v)) # 結果(流量)
b['Val'] = b.Var.apply(lambda v: value(v)) # 結果(設置するかどうか)
cst = value(lpDot(b.Dist, b.Var)) # 設置費用
val = value(m.objective) # 利便性
mxcst = cst - 1e-3 # 次の設置費用上限
h = nx.Graph()
h.add_edges_from([(r.Fr, r.To) for _, r in b[b.Val == 1].iterrows()])
res.append((cst, val, h))
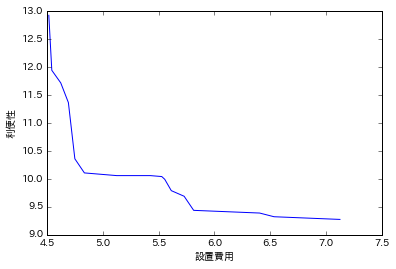
結果を見てみましょう。設置費用が上がるほど利便性がよくなります。
python
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['Hiragino Maru Gothic Pro', 'Yu Gothic']
plt.plot([r[0] for r in res], [r[1] for r in res])
plt.xlabel('設置費用')
plt.ylabel('利便性')
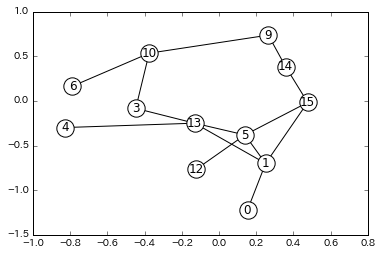
利便性が最も良い場合のグラフです。
python
draw(res[0][2])
以上