何をするのか
予約がいっぱいの繁盛レストランのオーナーから、売上を最大化して欲しいと頼まれました。
1日分の予約候補に対し、どれをOKにして、どれをキャンセルにするかを求めることにします。
このような問題も組合せ最適化で解くことができます。
予約は、下記のように時間と人数と単価がわかっているものとします。
1行が1つの予約に対応し、[開始時刻]に[人数]だけ来店し、[予約時間]の時間をかけて食事して、[単価]×[人数]払って帰るものとします。
| 開始時刻 | 予約時間 | 人数 | 単価 | |
| 0 | 13 | 2 | 2 | 2000 |
| 1 | 11 | 1 | 3 | 2800 |
| 2 | 16 | 3 | 3 | 2800 |
| ... | ... | ... | ... | ... |
座席について
レストランの座席は、2人テーブル×4 と4人テーブル×2の16人まで座れます。
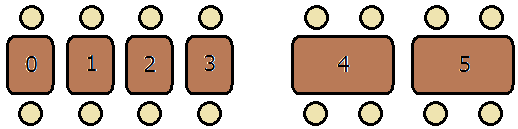
また、2人テーブル同士と4人テーブル同士は、くっつけて使うこともできます。
くっつけ方(以下テーブルグループとよぶ)は以下の13通りです。(番号はテーブル番号)
[0]
[1]
[2]
[3]
[4]
[5]
[0, 1]
[1, 2]
[2, 3]
[4, 5]
[0, 1, 2]
[1, 2, 3]
[0, 1, 2, 3]
定式化
| $\mbox{objective}$ | $\sum_i{\sum_j{人数_i 単価_i x_{ij}}}$ | 総売上 |
| $\mbox{variables}$ | $x_{ij} \in \{0, 1\} ~ \forall i, j$ | 予約$i$がテーブルグループ$j$を使うかどうか |
| $\mbox{subject to}$ | $\sum_j{x_{ij}} \le 1 ~ \forall i$ | 何れかのテーブルグループ |
| $テーブルグループjの座席数 \lt 予約iの人数のとき$ | 人数制限 | |
| $x_{ij} = 0 ~ \forall i, j$ | ||
| 同テーブル同時刻には、1組しか予約受入できない | ||
ただし、添字の意味は下記の通りとします。
i: 予約
j: テーブルグループ
s: テーブル
t: 時刻
Pythonで解く
まず、予約表(a)を乱数で作成します。
python
import numpy as np, numpy.random as rnd, pandas as pd, matplotlib.pyplot as plt
from pulp import *
def addvar(lowBound=0, count=[0], *args, **kwargs):
count[0] += 1
return LpVariable('v%d' % count[0], lowBound=lowBound, *args, **kwargs)
rnd.seed(5)
a = pd.DataFrame([(rnd.randint(10, 17), rnd.choice([1, 2, 2, 3]),
max(1, min(8, int(rnd.lognormal(1.2, 0.5)))), rnd.randint(10, 16) * 200)
for _ in range(60)], columns=['開始時刻', '予約時間', '人数', '単価'])
cap = [2, 2, 2, 2, 4, 4] # テーブル別座席数
sps = [[0], [1], [2], [3], [4], [5], [0, 1], [1, 2], [2, 3],
[4, 5], [0, 1, 2], [1, 2, 3], [0, 1, 2, 3]] # テーブルグループ別テーブルリスト
ns, nt = len(sps), 19 - 10 # テーブルグループ数、時刻数
定式化して解きます。
python
m = LpProblem(sense=LpMaximize) # 数理モデル
p = [[[] for t in range(nt)] for _ in range(6)] # テーブル別時刻別変数リスト
a['Var'] = [[addvar(cat=LpBinary) for j in range(ns)] for i, r in a.iterrows()]
m += lpDot(a.人数 * a.単価, a.Var.apply(lpSum)) # 目的関数(総売上)
for i, r in a.iterrows():
m += lpSum(r.Var) <= 1 # 何れかのテーブルグループ
for j, sp in enumerate(sps):
if sum(cap[s] for s in sp) < r.人数:
m += r.Var[j] == 0 # 人数制限
for s in sp:
for t in range(r.予約時間):
p[s][r.開始時刻 - 10 + t].append(r.Var[j])
for s in range(6):
for t in range(nt):
if p[s][t]:
m += lpSum(p[s][t]) <= 1 # 同テーブル同時刻には、1組しか予約受入できない
m.solve()
a['Val'] = a.Var.apply(lambda v: int(value(lpDot(range(1, ns+1), v))))
print('%s %d人 %.2f 万円' % (LpStatus[m.status],
sum(a[a.Val > 0].人数), value(m.objective) / 10000))
>>>
Optimal 83人 20.44 万円
売上は20万強ですね。成立した予約を表示します。
python
print('時間 人数 料金 テーブル')
for i, r in a.iterrows():
if r.Val:
print('%2d-%2d %d %d %s' % (r.開始時刻, r.開始時刻 + r.予約時間 - 1,
r.人数, r.人数 * r.単価, sps[r.Val-1]))
>>>
時間 人数 料金 テーブル
11-11 3 8400 [2, 3]
16-18 3 8400 [5]
13-13 4 11200 [4]
16-17 2 4800 [2]
16-17 4 11200 [4]
12-12 3 7200 [5]
14-15 8 20800 [4, 5]
14-14 2 4800 [2]
10-10 1 3000 [0]
16-18 2 6000 [3]
15-15 8 16000 [0, 1, 2, 3]
11-11 3 8400 [0, 1]
10-10 2 4000 [4]
11-12 4 9600 [4]
16-18 4 8000 [0, 1]
13-13 2 5600 [0]
12-12 6 13200 [1, 2, 3]
10-11 4 8000 [5]
10-10 3 6600 [1, 2]
13-13 4 10400 [5]
13-13 2 6000 [1]
13-13 4 10400 [2, 3]
14-14 2 5200 [3]
14-14 3 7200 [0, 1]
以上