二層のニューラルネットワークを実装してみた

前回記事ニューラルネットワークについてメモの続き
二層のニューラルネットワークを作り，MNISTを学習してみた．
ゼロから作るDeepLearningの第4章を参考

TwoLayerNet.py

import numpy as np

class TwoLayerNet:
    
    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        #重みの初期化
        self.params = {}
        #784 * 50の重み行列
        self.params['W1'] = weight_init_std * np.random.randn(input_size,hidden_size)
        #50 * 10の重み行列
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size,output_size)
        #バイアス，隠れ層の数だけ
        self.params['b1'] = np.zeros(hidden_size)
        #バイアス，出力層の数だけ
        self.params['b2'] = np.zeros(output_size)
    
    def sigmoid(self,x):
        return 1 / (1 + np.exp(-x))
    
    def softmax(self,a):
        c = np.max(a)
        exp_a = np.exp(a - c)#オーバーフロー対策
        sum_exp_a = np.sum(exp_a)
        y = exp_a / sum_exp_a
        return y
    
    def _numerical_gradient_1d(self,f, x):
        h = 1e-4 # 0.0001
        grad = np.zeros_like(x)

        for idx in range(x.size):
            tmp_val = x[idx]
            x[idx] = float(tmp_val) + h
            fxh1 = f(x) # f(x+h)

            x[idx] = tmp_val - h 
            fxh2 = f(x) # f(x-h)
            grad[idx] = (fxh1 - fxh2) / (2*h)

            x[idx] = tmp_val # 値を元に戻す

        return grad


    def numerical_gradient(self,f, X):
        if X.ndim == 1:
            return self._numerical_gradient_1d(f, X)
        else:
            grad = np.zeros_like(X)

            for idx, x in enumerate(X):
                grad[idx] = self._numerical_gradient_1d(f, x)

            return grad

    def cross_entropy_error(self,y,t):
        if y.ndim == 1:
            t = t.reshape(1,t.size)
            y = y.reshape(1,y.size)
        batch_size = y.shape[0]
        return -np.sum(t * np.log(y)) / batch_size
    
    def predict(self,x):
        W1,W2 = self.params['W1'],self.params['W2']
        b1,b2 = self.params['b1'],self.params['b2']
        
        a1 = np.dot(x,W1) + b1 #a = Wx + b
        z1 = self.sigmoid(a1)
        a2 = np.dot(z1,W2) + b2
        z2 = self.softmax(a2)
        
        return z2
    
    def loss(self, x, t):
        y = self.predict(x)
        
        return self.cross_entropy_error(y,t)
    
    def gradient(self,x,t):
        loss_W = lambda W: self.loss(x,t)
        grads = {}
        grads['W1'] = self.numerical_gradient(loss_W,self.params['W1'])
        grads['W2'] = self.numerical_gradient(loss_W,self.params['W2'])
        grads['b1'] = self.numerical_gradient(loss_W,self.params['b1'])
        grads['b2'] = self.numerical_gradient(loss_W,self.params['b2'])
        
        return grads

これに対して，MNISTのデータからミニバッチ学習(大きさ50)を500回行った．

LearningMNIST.py

import numpy as np
from sklearn.datasets import fetch_mldata
from sklearn.preprocessing import OneHotEncoder

mnist = fetch_mldata('MNIST original', data_home=".")

x_train = mnist['data'][:60000]
t_train = mnist['target'][:60000]
train_loss_list = []

#データの正規化(0<=x<=1)を行う
x_train = x_train.astype(np.float64)
x_train /= x_train.max()

#one-hotベクトルに変換
t_train = t_train.reshape(1, -1).transpose()
encoder = OneHotEncoder(n_values=max(t_train)+1)
t_train = encoder.fit_transform(t_train).toarray()

#hyper parameter
iters_num = 500
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

#画像データが28x28のデータのため入力層が784，隠れ層が50，出力層がラベル数に合わせ10
network = TwoLayerNet(input_size=784,hidden_size=50,output_size=10)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size,batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    grad = network.gradient(x_batch,t_batch)
    
    for key in ('W1','W2','b1','b2'):
        network.params[key] -= learning_rate * grad[key]
        
    loss = network.loss(x_batch,t_batch)
    train_loss_list.append(loss)

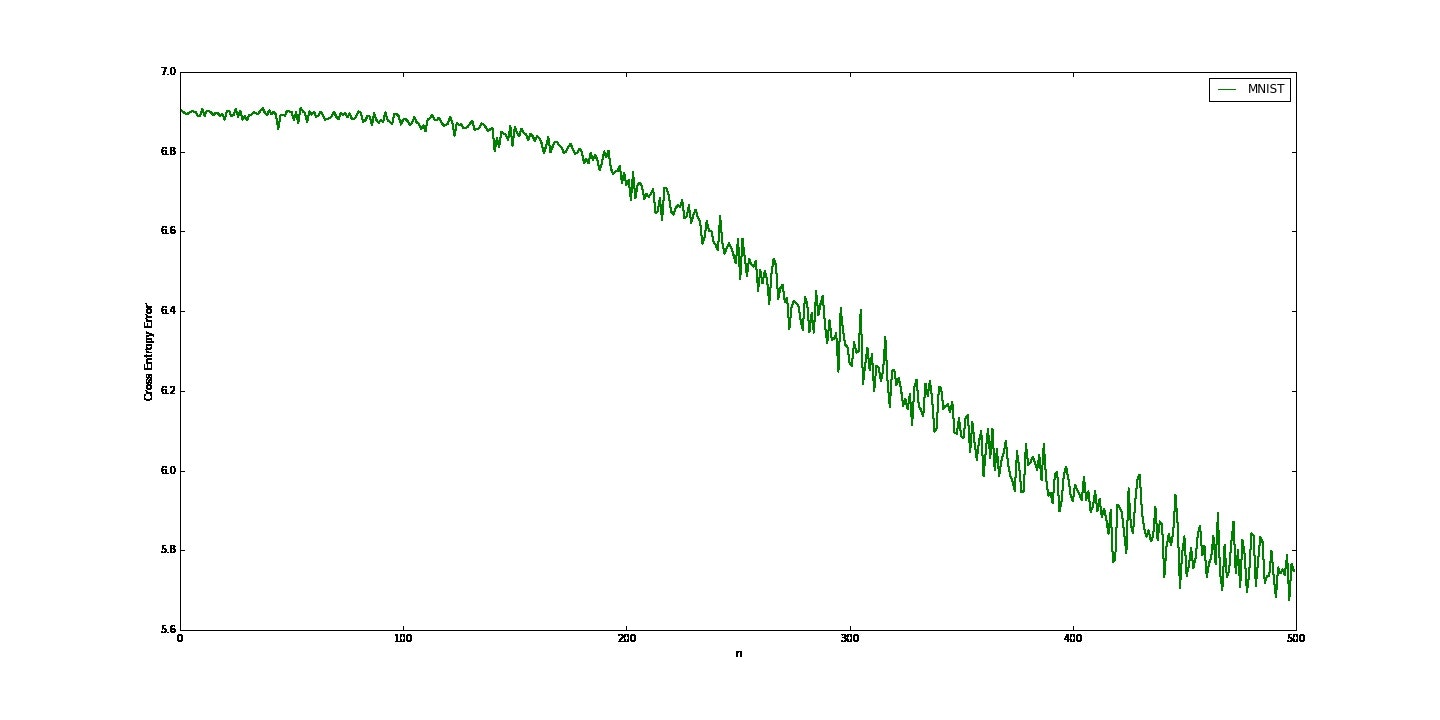
この結果が下のグラフ，縦軸が交差エントロピー誤差で横軸が学習の反復回数．

交差エントロピー誤差が減っている．
次回は，このニューラルネットワークの予測精度を確認する．