Christopher Olah氏のブログ記事
http://colah.github.io/posts/2014-07-Conv-Nets-Modular/
の翻訳です。
翻訳の誤りなどあればご指摘お待ちしております。
序論
ここ数年、ディープ・ニューラルネットワークは、コンピュータビジョン、音声認識などのさまざまなパターン認識の問題において、飛躍的な成果を達成しています。これらの成果に必須な要素の一つは、たたみ込みニューラルネットワークと呼ばれる特殊なニューラルネットワークでした。
たたみ込みニューラルネットワークは、基本的には、同じニューロンの多くの等価なコピーを使用した、ニューラルネットワークの一種と考えることができます。1 これは、学習すべき実際のパラメータ(すなわちニューロンの振る舞いを記述した値)の数をかなり小さく抑えたまま、ネットワークに多くのニューロンを持たせ、大規模な計算モデルを表現することができます。
同じニューロンの複数のコピーを持つというこのトリックは、大雑把にいうと、数学やコンピュータサイエンスにおける関数の抽象化に似ています。プログラミングの場合、関数を一度だけ記述し、多くの場所でそれを使用します。別々の場所に同じコードを100回書くことがないため、より速くプログラムでき、バグも減らします。同様に、たたみ込みニューラルネットワークは一度ニューロンを学習するだけで、多くの場所でそれを使用できます。これはモデルの学習を容易にし、エラーを減らします。
たたみ込みニューラルネットワークの構造
ニューラルネットワークに音声サンプルを与え、人間が話しているかそうでないかを予測したいとします。誰かが話している場合には、より多くの解析を行いたいかもしれません。
異なる時点でのオーディオサンプルを取得します。サンプルは等間隔であるとします。
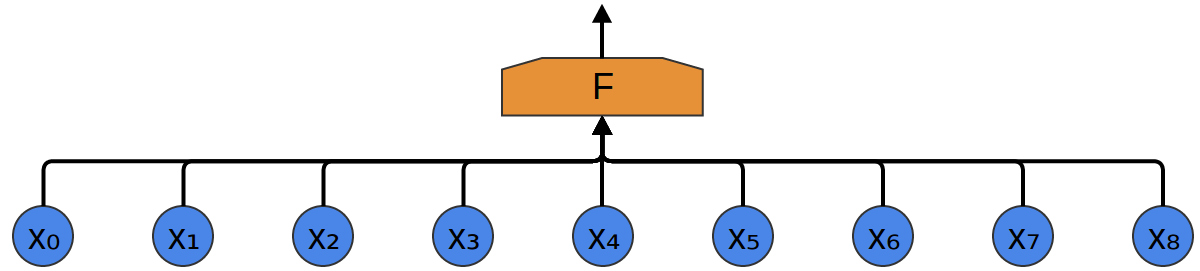
ニューラルネットワークでそれらを審理して分類する最も簡単な方法は、単に完全に結合された層にそれらすべてを結合することです。そこには多くの異なるニューロンがあり、すべての入力はすべてのニューロンと結合します。
より洗練されたアプローチは、データ内の、検索するために有用な性質の、ある種の対称性に気づきます。私たちは局所的な性質について特に関心をもちます:与えられた時点の周辺にどの周波数の音があるか?それは増加しているか、減少しているか? などです。
私たちは、時間内のすべての点において同じ性質に関心をもちます。冒頭の周波数を知ることは有用だし、途中の周波数を知ることも有用、終わりの周波数を知ることも有用です。ここでも、決定するにはオーディオサンプルの小さなウィンドウを見るだけでよい、局所的な性質であることに注意してください。
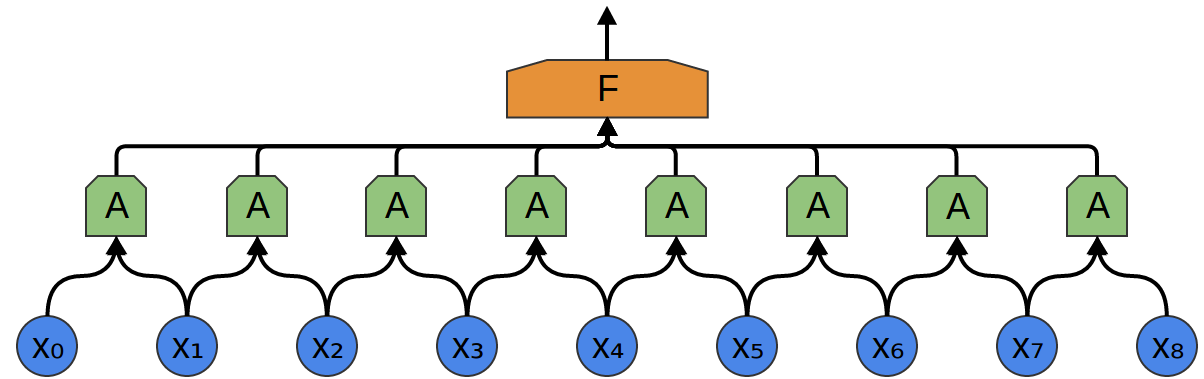
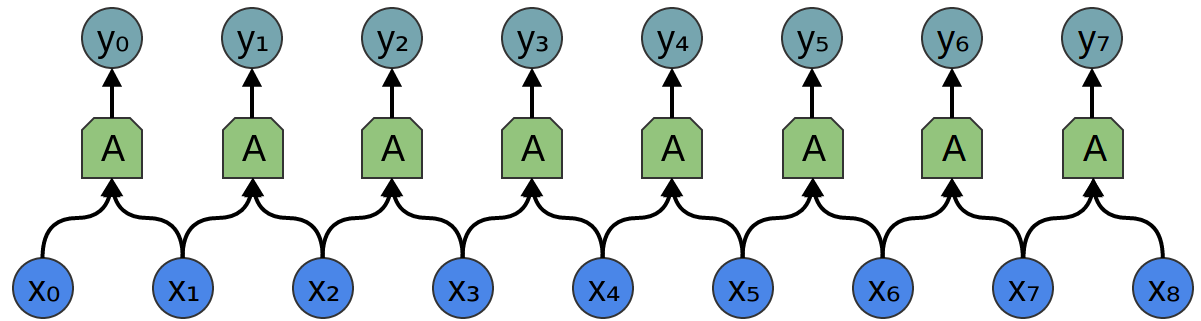
そこで、データの小さな時間セグメントを見る、ニューロンのグループ $A$ を作成することができます。2 $A$ は、そのようなすべてのセグメントを見て、特定の特徴量を計算します。そして、このたたみ込み層の出力は、全結合層 $F$ に供給されます。
上記の例では、$A$ は2点のみからなるセグメントを見ていました。これは現実的ではありません。通常、たたみ込み層のウィンドウははるかに大きいです。
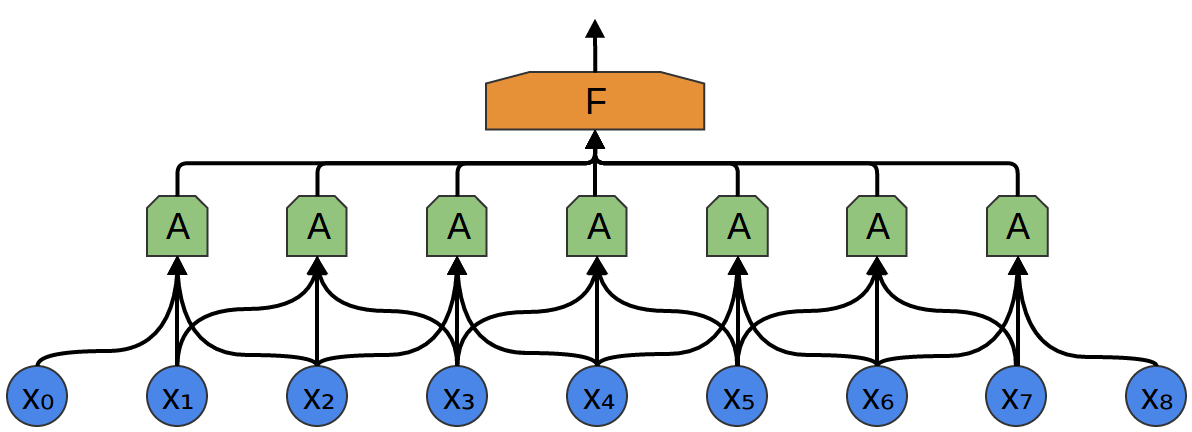
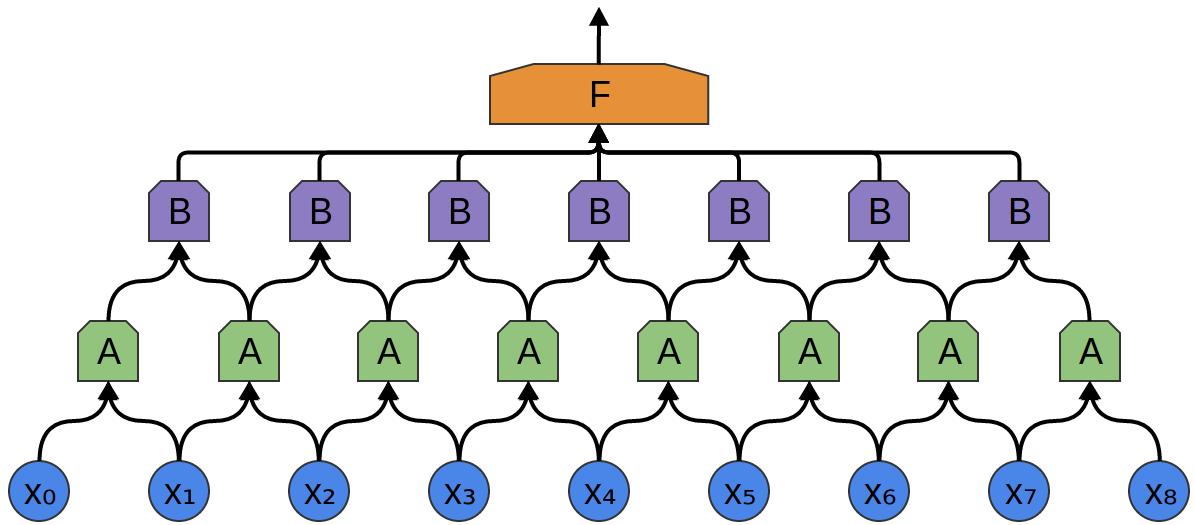
次の例では、$A$ は3点を見ます。これも現実的ではありません、悲しいことに、多くの点と結合する $A$ を可視化することは難しいです。
たたみ込み層のとても素晴らしい性質の1つは、合成可能だということです。1つのたたみ込み層の出力を、異なるものに供給することができます。各層では、ネットワークは、より高いレベル、より抽象的な特徴を検出することができます。
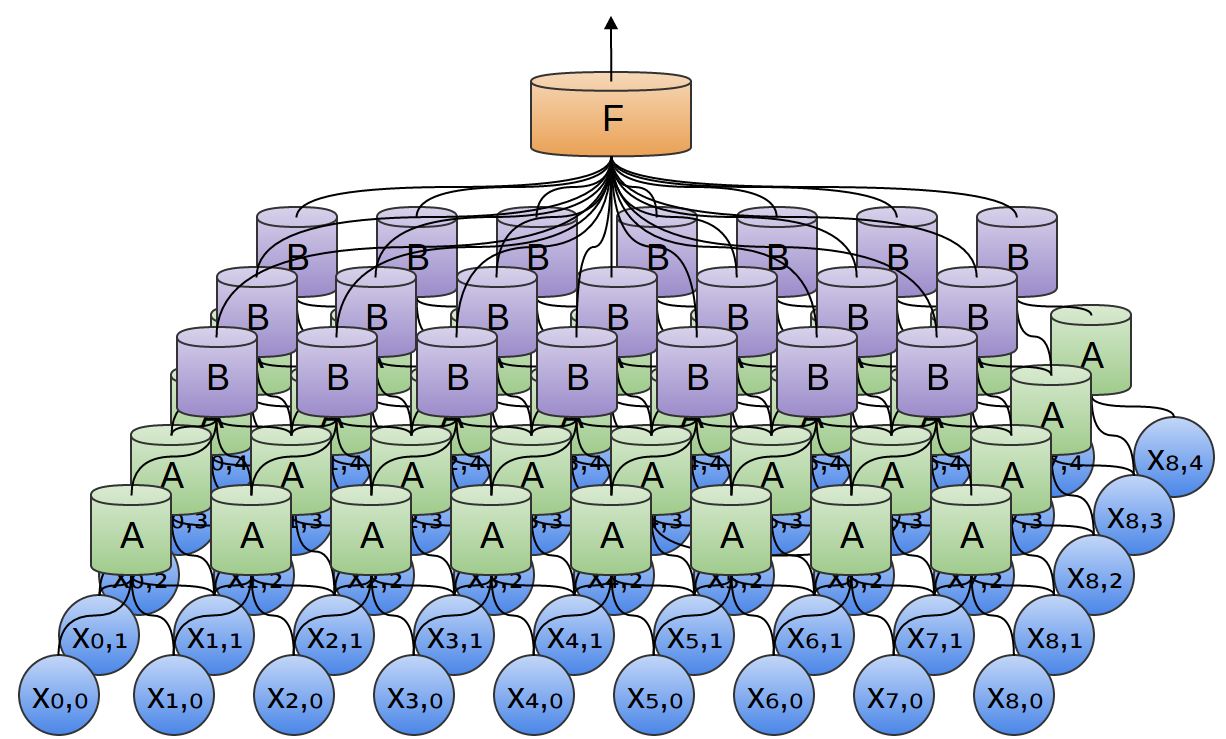
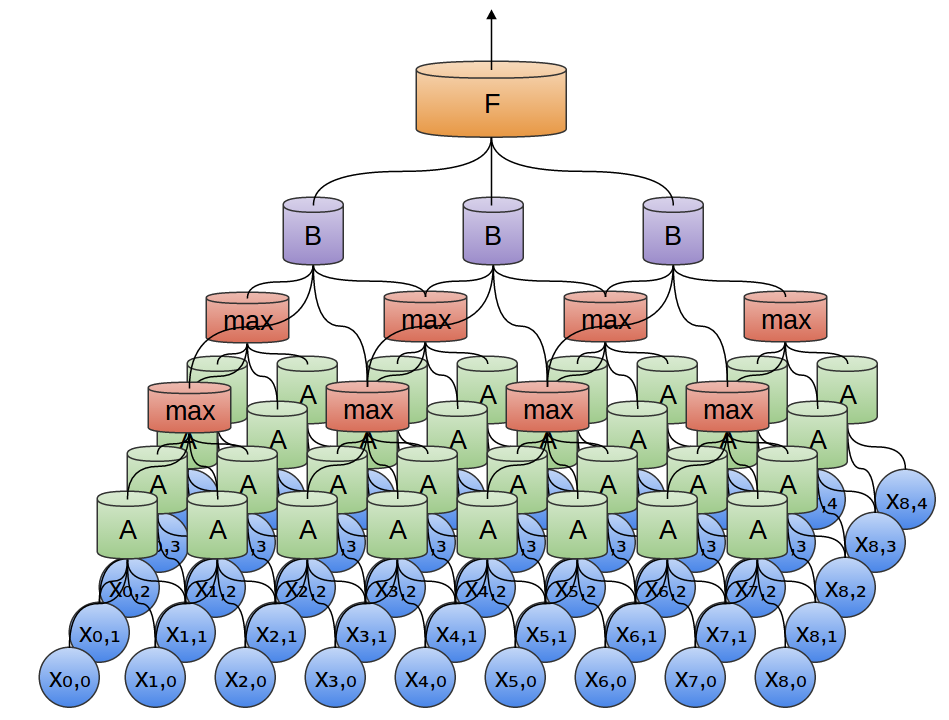
次の例には、ニューロンの新たなグループ $B$ があります。$B$ は、前の層に積み重ねられた別のたたみ込み層を形成するために使用されています。
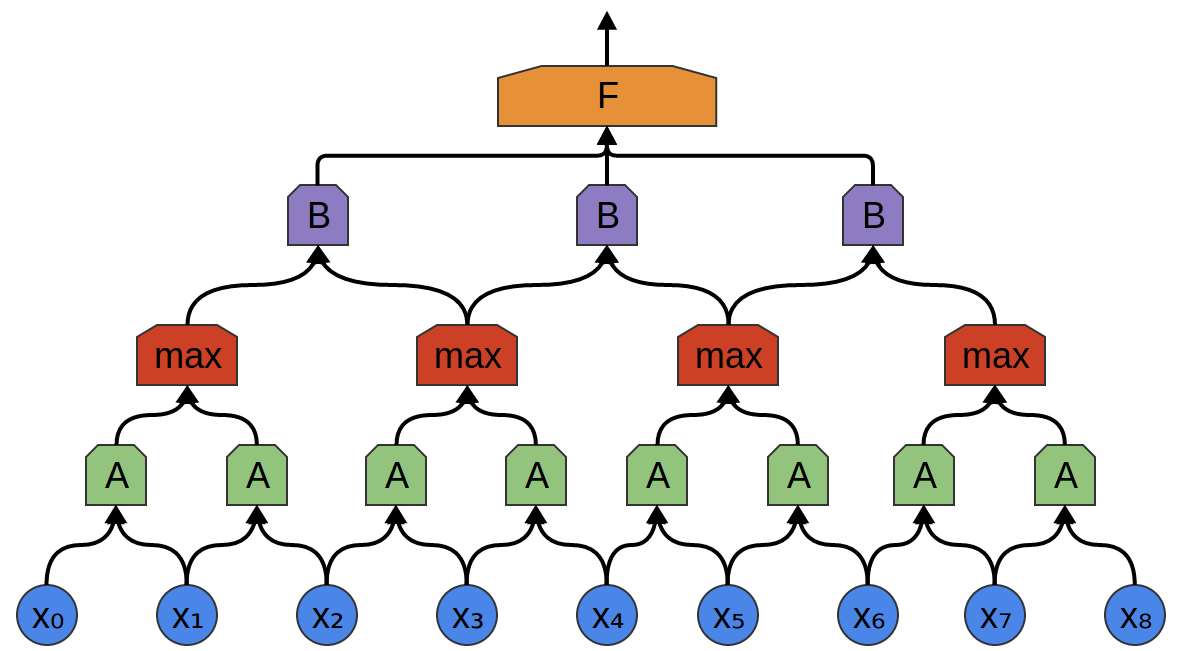
たたみ込み層は、多くの場合、プーリング層と交互に重ね合わされます。具体的には、最大値プーリング層と呼ばれる、非常に人気がある、層の一種です。
多くの場合、高レベルの観点から、特徴が存在する正確な時点は気になりません。周波数の変動がわずかに早くまたは遅く発生したとして、それは重要でしょうか?
最大値プーリング層は、前の層の小さなブロック内の特徴量の最大値をとります。出力は、特徴が前の層の領域に存在したかどうかは教えますが、正確な位置は教えてくれません。
最大値プーリング層は、「ズームアウト」の一種です。それらは、以降のたたみ込み層がデータのより大きなセクションに作用することを可能にします。なぜなら、プーリング層の後の小さなパッチは、層の前のより大きなパッチに対応するからです。それらはまた、私たちをデータの非常に小さな変化に対し不変にします。
前の例では1次元のたたみ込み層を使用しました。しかし、たたみ込み層は高次元データ上で動作することも同様にできます。実際、たたみ込みニューラルネットワークの最も有名な成功は、2次元たたみ込みニューラルネットワークの画像認識への適用です。
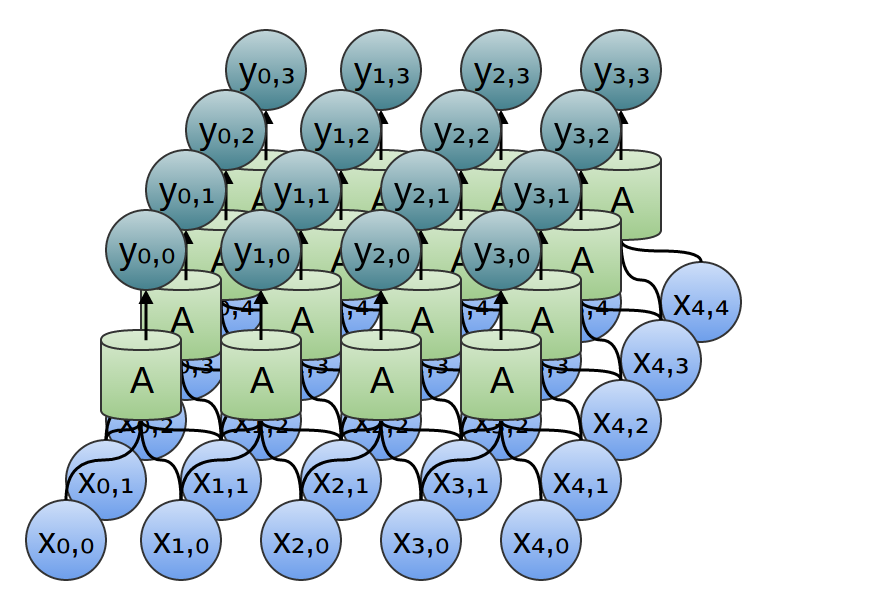
2次元のたたみ込み層では、$A$ はセグメントを見る代わりにパッチを見ます。
各パッチについて、$A$ は特徴量を計算します。例えば、それは、エッジの存在を検出することを学習するかもしれません。または、テクスチャの有無を検出することを学習するかもしれません。あるいは2色間のコントラストを。
前の例では、たたみ込み層の出力を全結合層の中に供給しました。しかし、1次元の場合におこなったように、2つのたたみ込み層を合成することもできます。
2次元で最大プーリングを行うこともできます。ここでは、小さなパッチ上の特徴量の最大値を取ります。
これは要するに、画像全体を考慮した場合、エッジの正確な位置をピクセル単位では気にしない、ということです。存在する場所を数ピクセル内で知るだけで十分です。
3次元のたたみ込みネットワークはまた、ビデオやボリュメトリックデータ(例えば、3次元医療スキャン)のようなデータのためにも、使用されています。しかし、あまり幅広くは使用されおらず、また、可視化ははるかに困難です。
以前、$A$ はニューロンのグループだと言いました。このことについてもう少し正確にしなければなりません:$A$ は正確には何でしょうか?
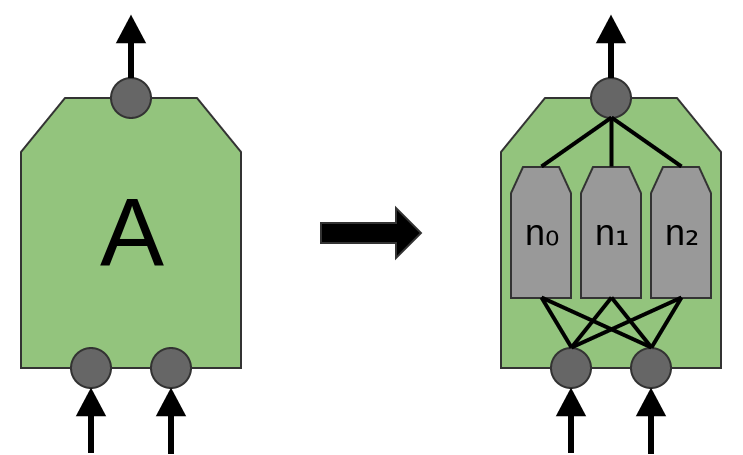
伝統的なたたみ込み層において、$A$ は並行な多くのニューロンです。全てが同じ入力を得て、異なる特徴量を計算します。
例えば、2次元のたたみ込み層で、1つのニューロンが水平エッジを検出し、別のものが垂直エッジを検出するかもしれないし、他のものは緑と赤のコントラストを検出するかもしれません。
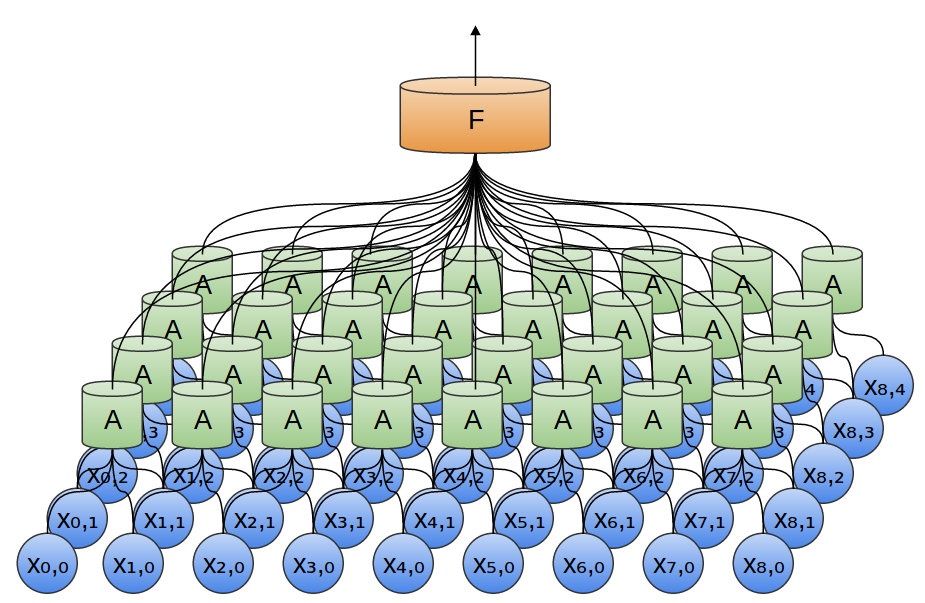
最近の論文「Network in Network」(Lin et al. (2013))では、新たな「Mlpconv」層が提案された、と言われています。このモデルでは、$A$ はニューロンの複数の層を持ち、最後の層は領域のより高いレベルの特徴を出力します。論文では、モデルは、複数のベンチマークデータセットで新たなステート・オブ・ジ・アートを達成する、いくつかの非常に目覚ましい成果を成し遂げています。
この記事の目的として、標準的なたたみ込み層に焦点を当てる、と述べました。それを検討する準備は整いました!
たたみ込みニューラルネットワークの成果
先ほど、たたみ込みニューラルネットワークを用いた、コンピュータビジョンにおける最近のブレークスルーに言及しました。先へ進む前に、モチベーションとして、これらの結果のいくつかを簡単に議論したいと思います。
2012年、Alex Krizhevsky、Ilya Sutskever、そして Geoff Hinton は、画像分類の成果により世の中を非常に驚かせました(Krizehvsky et al. (2012))。
その進歩は異なる複数のピースを一緒に組み合わせることの結果でした。彼らは非常に大規模な、深い、ニューラルネットワークを訓練するためにGPUを使用しました。そして、新たな種類のニューロン(ReLU)と、「過学習」と呼ばれる問題を軽減するための新たな技術(ドロップアウト)を使用しました。また、多くの画像カテゴリを持つ非常に大規模なデータセット(ImageNet)を使用しました。そして、もちろん、それはたたみ込みニューラルネットワークでした。
以下に示すそのアーキテクチャは、とても深いです。これは、散在するプーリングを伴う5つのたたみ込み層、3 および3つの全結合層を持ちます。初めの方の層は、2つのGPUに分割されています。
彼らは千の異なるカテゴリに画像を分類するようにネットワークを訓練しました。
ランダムに推測すると、正解は0.1%です。 Krizhevskyらのモデルは、63%の正答率です。さらに、トップ5の解答に正解が含まれるのは85%です!

上:4つの正しい分類例。下:4つの誤った分類例。それぞれの例には、画像に続いてそのラベル、さらに確率を伴ったトップ5の推測を示しています。Krizehvsky et al. (2012)より。
そのエラーの一部さえ、私にはかなり合理的に思われます!
また、ネットワークの第1層が学習することを調べることができます。
たたみ込み層が2つのGPUの間で分割されたことを思い出してください。情報は各層を行き来しておりませんので、分割された両側は現実の方法で切断されています。モデルが実行されるたびに、双方が特化することがわかりました。

最初のたたみ込み層によって学習されたフィルタ。上半分が1つのGPUの層に対応し、下半分が他の層に相当。Krizehvsky et al. (2012)より
一方の側のニューロンは、異なる向きや大きさのエッジを検出することを学習し、黒と白に焦点を当てます。反対側のニューロンは、色のコントラストやパターンを検出し、色と質感に特化しています。4 ニューロンがランダムに初期化されることに注意してください。誰もエッジ検出器であるように設定したり、このように分割していません。これは、画像を分類するためのネットワークの訓練から単に生じたものです。
これらの顕著な成果(そして、当時のその周辺の他の刺激的な結果)は、ほんの始まりでした。すぐに、変更したアプローチをテストし、結果を改善し、または他の分野に応用した、多くの他の研究が続きました。そして、ニューラルネットワークのコミュニティに加えて、コンピュータビジョンのコミュニティの多くは、深いたたみ込みニューラルネットワークを採用しています。
たたみ込みニューラルネットワークは、コンピュータビジョンと近年のパターン認識に必須のツールです。
たたみ込みニューラルネットワークの定式化
入力 ${x_n}$ と出力 ${y_n}$ を持つ1次元のたたみ込み層を考えましょう:
出力を入力の式で表すことは比較的簡単です:
y_n = A(x_{n}, x_{n+1}, ...)
例えば、上記の中で:
y_0 = A(x_0, x_1)
y_1 = A(x_1, x_2)
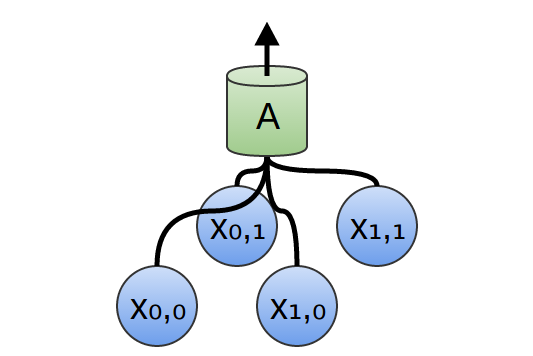
同様に、入力 ${x_{n,m}}$ および出力 ${y_{n,m}}$ を持つ2次元のたたみ込み層の場合:
再び、出力を入力の式で書くことができます:
y_{n,m} = A\left(\begin{array}{ccc} x_{n,~m}, & x_{n+1,~m},& ...,~\\ x_{n,~m+1}, & x_{n+1,~m+1}, & ..., ~\\ &...\\\end{array}\right)
例えば:
y_{0,0} = A\left(\begin{array}{cc} x_{0,~0}, & x_{1,~0},~\\ x_{0,~1}, & x_{1,~1}~\\\end{array}\right)
y_{1,0} = A\left(\begin{array}{cc} x_{1,~0}, & x_{2,~0},~\\ x_{1,~1}, & x_{2,~1}~\\\end{array}\right)
これを $A(x)$ の式と組み合わせると、
A(x) = \sigma(Wx + b)
少なくとも理論的には、たたみ込みニューラルネットワークの実装に必要なすべてが得られます。
実際には、これは多くの場合たたみ込みニューラルネットワークを考えるための最良の方法ではありません。たたみ込みと呼ばれる数学的演算の用語による、代わりの定式化があり、多くの場合より便利です。
たたみ込み演算は強力なツールです。数学では、偏微分方程式の研究から、確率論に至るまで、多様な文脈で出てきます。一つには偏微分方程式におけるその役割のため、たたみ込みは物理科学で非常に重要です。また、コンピュータグラフィックスおよび信号処理のような多くの適用分野で重要な役割を担っています。
私たちにとって、たたみ込みは多くの利点を提供します。第一に、単純な観点に示唆されるものより、はるかに効率的なたたみ込み層の実装を作成できるようになります。第二に、今の定式化から、xのインデックスに現れるすべてを記述する多くの煩雑さを取り除きます。今の定式化はあまり複雑に見えないかもしれませんが、それは私たちがまだ扱いにくい例までたどり着いていないからです。最後に、たたみ込みは、たたみ込み層について説明するための著しく異なる視点を与えるでしょう。
“私はあなたの計算方法の優雅さを賞賛します。我々のような者が苦労して徒歩で道を行く一方で、真の数学という馬に乗って荒野を駆け抜けるのですから、それは素晴らしいでしょう。 - アルバート・アインシュタイン
このシリーズの次の記事
この記事は、たたみ込みニューラルネットワークとその一般化のシリーズの一部です。最初の2つの記事は、ディープラーニングに精通した方のためのレビューですが、最後の1つは、誰にでも興味があるもののはずです。最新版を得るためには、私のRSSフィードを購読してください!
下または横にコメントしてください。github 上でプルリクエストすることができます。
謝辞
コメントとサポートをしてくださった、Eliana Lorch、Aaron Courville、Sebastian Zany に深く感謝しています。
-
同じニューロンの複数のコピーを使用するすべてのニューラルネットワークが、たたみ込みニューラルネットワークではないことに留意すべきです。たたみ込みニューラルネットワークは、より一般的なトリック、*重み結束(weight-tying)*を使用したニューラルネットワークの一種です。これを行う他の種類のニューラルネットワークは、リカレントニューラルネットワークと再帰的ニューラルネットワークです。 ↩
-
$A$ のように、複数の場所に現れるニューロンのグループは、モジュールと呼ばれ、それらを使用するネットワークは、モジュラー・ニューラルネットワークと呼ばれることがあります。 ↩
-
彼らはまた、論文で7つの層を使用したテストをしています。 ↩
-
これは、網膜の桿体および錐体に興味深い類似点を持っているようです。 ↩