More than 5 years have passed since last update.

Lua版ゼロから作るDeep Learning その２［活性化関数］

Last updated at 2017-06-04Posted at 2017-06-04

過去記事

Lua版ゼロから作るDeep Learning その１[パーセプトロンの実装]

活性化関数の実装

　今回は活性化関数（ステップ関数・シグモイド関数・ReLU 関数）の実装です。

　スクリプトは以下の通りです。

activationFunc.lua

require 'gnuplot'

---ステップ関数.
-- 入力の各成分が０を超えたときに１を返す
-- @param x 入力 (Type：torch.DoubleTensor)
-- @return 1 or 0 (Type：torch.ByteTensor)
function step_function(x)
    local y = torch.gt(x, 0)    -- '>' 演算子の代わり
    return y
end

---シグモイド関数.
-- 入力の各成分に対するゲイン1の標準シグモイド関数（1/(1+exp(x))）の値を返す
-- @param x 入力 (Type：torch.DoubleTensor)
-- @return torch.DoubleTensor
function sigmoid(x)
    y = x:clone():fill(1)
    return torch.cdiv(y , (1 + torch.exp(-x)))
end

---ReLU(Rectified Linear Unit)関数.
-- 入力の各成分が0以下ならば0、0よりも高いならばそのままの値を返す
-- @param x 入力 (Type：torch.DoubleTensor)
-- @return torch.DoubleTensor
function relu(x)
    y = x:clone():fill(0)
    return torch.cmax(y, x)
end

--確認

print("ステップ関数")
print("step_function(torch.Tensor({-1.0, 1.0, 2.0})):")
print(step_function(torch.Tensor({-1.0, 1.0, 2.0})))

local x = torch.range(-5.0, 5.0, 0.1)
local y = step_function(x)
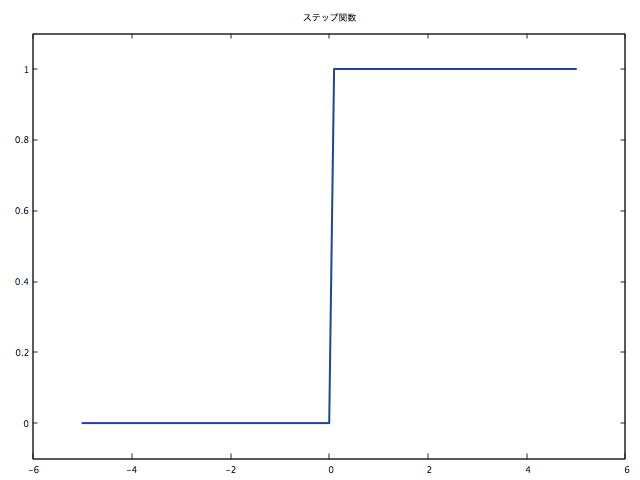
gnuplot.figure(1)
gnuplot.title('ステップ関数')
gnuplot.axis({torch.min(x)-1, torch.max(x)+1, -0.1, 1.1})
gnuplot.plot(x, y, '-')


print("シグモイド関数")
print("sigmoid(torch.Tensor({-1.0, 1.0, 2.0})):")
print(sigmoid(torch.Tensor({-1.0, 1.0, 2.0})))

local x = torch.range(-5.0, 5.0, 0.1)
local y = sigmoid(x)
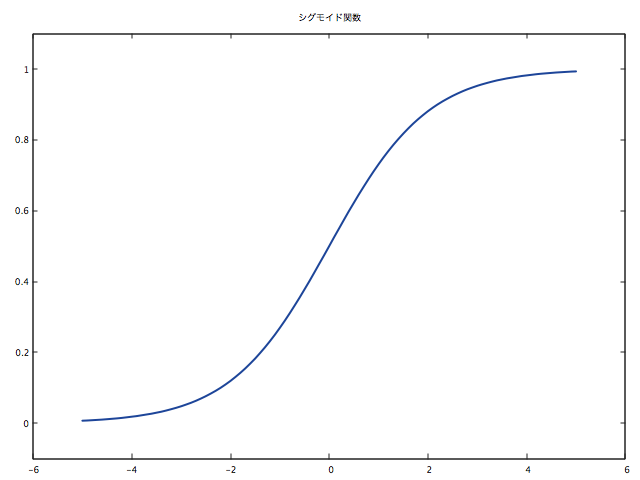
gnuplot.figure(2)
gnuplot.title('シグモイド関数')
gnuplot.axis({torch.min(x)-1, torch.max(x)+1, -0.1, 1.1})
gnuplot.plot(x, y, '-')

local x = torch.range(-5.0, 5.0, 0.1)
local y1 = step_function(x)
local y2 = sigmoid(x)
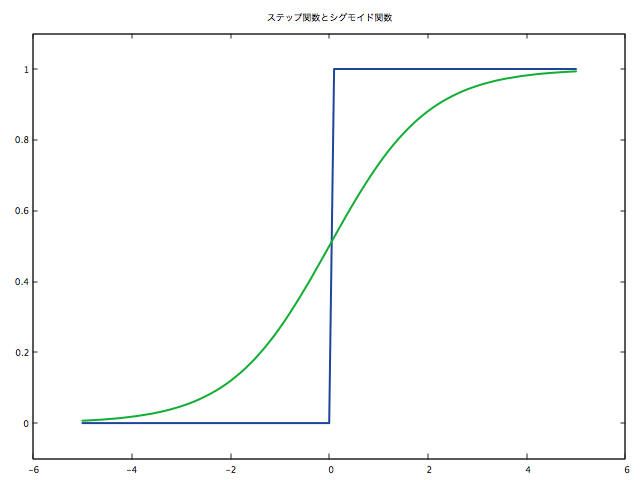
gnuplot.figure(3)
gnuplot.title('ステップ関数とシグモイド関数')
gnuplot.axis({torch.min(x)-1, torch.max(x)+1, -0.1, 1.1})
gnuplot.plot({x, y1, '-'}, {x, y2, '-'})

print("ReLU(Rectified Linear Unit) 関数")
print("sigmoid(torch.Tensor({-1.0, 1.0, 2.0})):")
print(relu(torch.Tensor({-1.0, 1.0, 2.0})))

local x = torch.range(-5.0, 5.0, 0.1)
local y = relu(x)
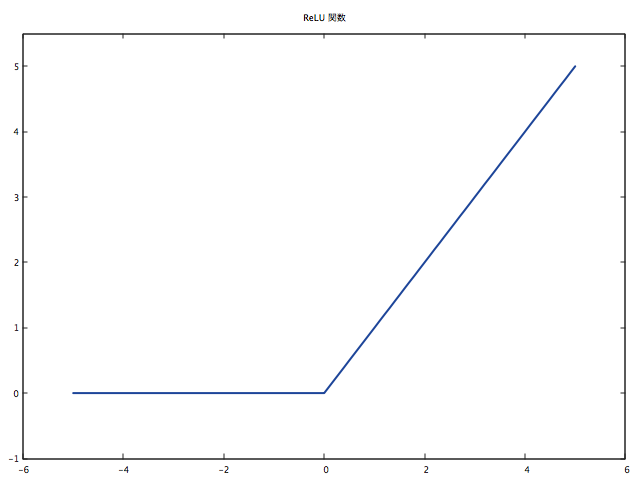
gnuplot.figure(4)
gnuplot.title('ReLU 関数')
gnuplot.axis({torch.min(x)-1, torch.max(x)+1, -1, 5.5})
gnuplot.plot(x, y, '-')

　python の numpy では各要素と数値との商は演算子 '/' で大丈夫でしたが、Torchでは同様のオーバーロードは実装されていないようです。
　したがって、シグモイド関数は以下のように書かなくてはなりません。

sigmoid関数の実装部分

function sigmoid(x)
    --入力したTensorのコピーの全要素を1に書き換える
    y = x:clone():fill(1) 
    --各要素同士の商を求める
    return torch.cdiv(y , (1 + torch.exp(-x)))
end

　これは numpy よりも少しまどろっこしいかもしれません。

　ただ演算子のオーバーロードは、可読性は向上しますが、変数の型がわかりづらくなるためにうっかりミスに繋がりやすいです。

　なのでこのあたりは一長一短ではないかと思います。

　個人的にはこっちのほうが好きです。

　また同じような例として、Torch のTensor では論理演算子が使えません。代わりに以下のように書きます。

ステップ関数の実装部分

function step_function(x)
    local y = torch.gt(x, 0)    -- '>' 演算子の代わり
    return y
end

　戻り値はintenger 型のTensor となります。

　論理演算子の代替メソッド一覧は以下の通りです。

Tensorに対する論理演算メソッド

torch.lt(a, b) -- '<'
torch.le(a, b) -- '<='
torch.gt(a, b) -- '>'
torch.ge(a, b) -- '>='
torch.eq(a, b) -- '=='
torch.ne(a, b) -- '~='

　詳しくは以下のマニュアルをご参照ください。

　Math Functions

実行

　では先ほどのスクリプトを実行します。

activationFunc.luaの実行

th activationFunc.lua

　出力は以下の通りです。

標準出力

ステップ関数	
step_function(torch.Tensor({-1.0, 1.0, 2.0})):	
 0
 1
 1
[torch.ByteTensor of size 3]

シグモイド関数	
sigmoid(torch.Tensor({-1.0, 1.0, 2.0})):	
 0.2689
 0.7311
 0.8808
[torch.DoubleTensor of size 3]

ReLU(Rectified Linear Unit) 関数	
sigmoid(torch.Tensor({-1.0, 1.0, 2.0})):	
 0
 1
 2
[torch.DoubleTensor of size 3]