はじめに
前回の記事で学習アルゴリズムを使ってオーバーフィッティングを解決したいと言ったため、今回は学習アルゴリズムの1つであり、最近流行っているディープラーニング(以降DL)について紹介しようと思います。
似たようなアルゴリズムでニューラルネットワーク(以降NN)があるため、まずは両者の違いについて説明した後、例題として論理回路を学習、予測まで行うのでよろしくお願いします。
NNとDLの違いについて
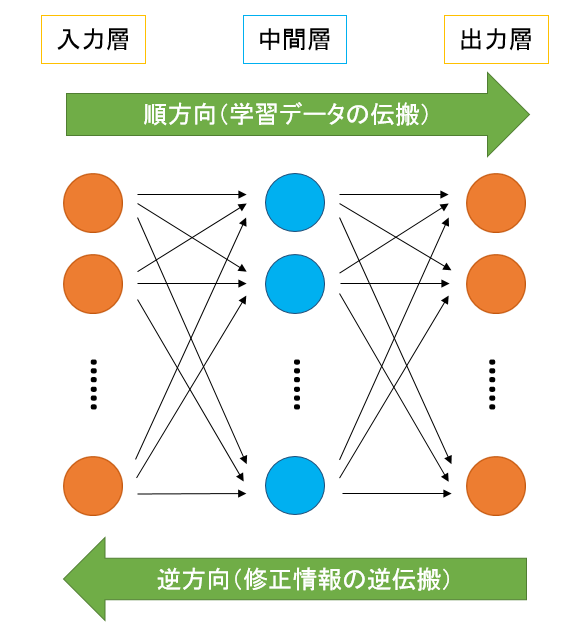
まずはNNについて説明します。NNは人間が持つ脳神経回路の動きを模倣した学習アルゴリズムになります。生物の神経系をヒントに作られているため、多数のニューロンが結合し合うネットワーク構造になっています。
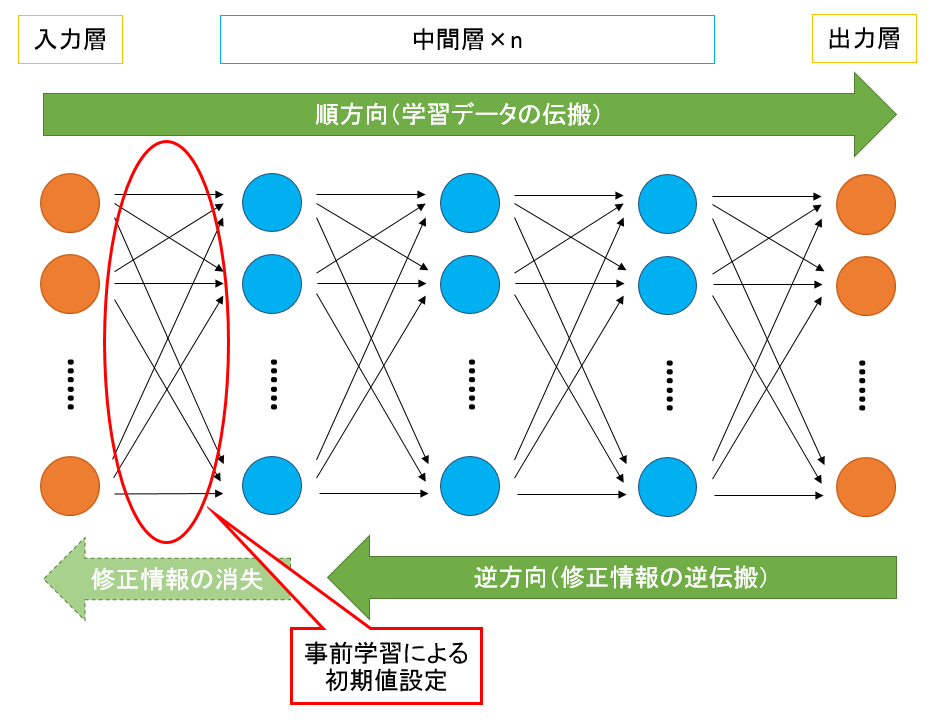
一方、DLですが、こちらはNNを多層化したものになっています。通常、NNの多層化を行うと誤差情報の伝搬が途中で消えてしまう、あるいは時間がかかりすぎてしまい学習が成立しない事が多かったのですが、近年は事前学習による結合荷重の初期値設定やコンピュータの性能向上により改善されてきました。NNとDLのネットワーク構造を図に示すと次のようになります。
論理回路の学習
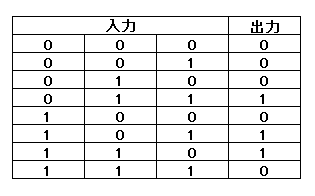
それでは実際にDLを使ってみる事にしましょう。今回ですが、3入力1出力の論理回路を例題として扱う事にします。真理値表については次のものを使用しました。
表1のうち上から数えていって6つ目までを学習に使用し、残りの2つを予測として使う事にします。また、DLで設定したパラメータは次のようになります。各項目は説明すると長くなるため、本記事では省略します。興味のある方は調べてみてください。
表2:パラメータ設定
| 項目 | 内容 |
|---|---|
| 学習回数 | 10000 |
| 訓練データ数 | 6 |
| 入力層の数 | 3 |
| 中間層1の数 | 4 |
| 中間層2の数 | 2 |
| 出力層の数 | 1 |
| 学習係数ε | 0.3 |
| 慣性係数α | 1 |
上記のパラメータ項目にも書いてありますが、今回は4層のネットワークで学習の方を行っていきたいと思います。4層のネットワークによるDLのソースコードについては次のようになります。
/* プログラム名:deeplearn.c */
/* ディープラーニング(学習) */
# include<stdio.h>
# include<stdlib.h>
# include<math.h>
# include<time.h>
/* パラメータを設定する(今書いてある値は例であるため、好きに設定してよい) */
# define NUM_LEARN 10000 /* 学習回数 */
# define NUM_SAMPLE 6 /* 訓練データ数(今回は6パターン用意する)*/
# define NUM_INPUT 3 /* 入力層の数(論理回路の入力)*/
# define NUM_HIDDEN_ONE 4 /* 中間層1の数(自由)*/
# define NUM_HIDDEN_TWO 2 /* 中間層2の数(自由)*/
# define NUM_OUTPUT 1 /* 出力層の数(論理回路の出力)*/
# define EPSILON 0.3 /* 学習係数ε */
# define ALPHA 1 /* 慣性係数α ※振動を避けるために設定するものであるが、基本的に1に設定しておけば問題なし */
/* シグモイド関数 */
double sigmoid(double x){
double f;
f=1.0/(1.0+exp(-x));
return f; /* 戻り値が関数値 */
}
int tx[NUM_SAMPLE][NUM_INPUT],ty[NUM_SAMPLE][NUM_OUTPUT]; /* txが入力、tyが出力 教師データを格納する */
double x[NUM_INPUT+1],h1[NUM_HIDDEN_ONE+1],h2[NUM_HIDDEN_TWO+1],y[NUM_OUTPUT]; /* xが入力、h1が中間1、h2が中間2、yが出力 それぞれニューロンの値。+1は閾値表現用 */
double w1[NUM_INPUT+1][NUM_HIDDEN_ONE],w2[NUM_HIDDEN_ONE+1][NUM_HIDDEN_TWO],w3[NUM_HIDDEN_TWO+1][NUM_OUTPUT]; /* w1が入力ー中間1、w2が中間1ー中間2、w3が中間2ー出力の結合荷重の値 */
double h1_back[NUM_HIDDEN_ONE+1],h2_back[NUM_HIDDEN_TWO+1],y_back[NUM_OUTPUT]; /* h1_backが中間1、h2_backが中間2、y_backが出力の逆伝播量 */
int main(void){
int ilearn,isample,i,j;
double net_input,epsilon,alpha;
srand((unsigned)time(NULL));
epsilon=(double)EPSILON;
alpha=(double)ALPHA;
/* 教師データの設定(6パターンの入力とそれに対応する出力値を設定) */
tx[0][0]=0;
tx[0][1]=0;
tx[0][2]=0;
ty[0][0]=0;
tx[1][0]=0;
tx[1][1]=0;
tx[1][2]=1;
ty[1][0]=0;
tx[2][0]=0;
tx[2][1]=1;
tx[2][2]=0;
ty[2][0]=0;
tx[3][0]=0;
tx[3][1]=1;
tx[3][2]=1;
ty[3][0]=1;
tx[4][0]=1;
tx[4][1]=0;
tx[4][2]=0;
ty[4][0]=0;
tx[5][0]=1;
tx[5][1]=0;
tx[5][2]=1;
ty[5][0]=1;
/* 結合荷重にランダムな初期値を設定 */
for(i=0;i<NUM_INPUT+1;i++){
for(j=0;j<NUM_HIDDEN_ONE;j++){
w1[i][j]=(double)rand()/RAND_MAX/1.0;
}
}
for(i=0;i<NUM_HIDDEN_ONE+1;i++){
for(j=0;j<NUM_HIDDEN_TWO;j++){
w2[i][j]=(double)rand()/RAND_MAX/1.0;
}
}
for(i=0;i<NUM_HIDDEN_TWO+1;i++){
for(j=0;j<NUM_OUTPUT;j++){
w3[i][j]=(double)rand()/RAND_MAX/1.0;
}
}
/* 学習の繰り返し */
for(ilearn=0;ilearn<NUM_LEARN;ilearn++){
printf("\n学習回数:%d回目\n",ilearn+1);
/* 訓練データの繰り返し */
for(isample=0;isample<NUM_SAMPLE;isample++){
/* 順方向の動作 */
/* 訓練データに従って、ネットワークへの入力設定 */
for(i=0;i<NUM_INPUT;i++){
x[i]=tx[isample][i];
}
/* 閾値設定x */
x[NUM_INPUT]=(double)1.0;
/* 隠れ素子1の計算 */
for(j=0;j<NUM_HIDDEN_ONE;j++){
net_input=0;
for(i=0;i<NUM_INPUT+1;i++){
net_input=net_input+w1[i][j]*x[i];
}
/* シグモイドの適用 */
h1[j]=sigmoid(net_input);
}
/* 閾値設定h1 */
h1[NUM_HIDDEN_ONE]=(double)1.0;
/* 隠れ素子2の計算 */
for(j=0;j<NUM_HIDDEN_TWO;j++){
net_input=0;
for(i=0;i<NUM_HIDDEN_ONE+1;i++){
net_input=net_input+w2[i][j]*h1[i];
}
/* シグモイドの適用 */
h2[j]=sigmoid(net_input);
}
/* 閾値設定h2 */
h2[NUM_HIDDEN_TWO]=(double)1.0;
/* 出力素子の計算 */
for (j=0;j<NUM_OUTPUT;j++){
net_input=0;
for(i=0;i<NUM_HIDDEN_TWO+1;i++){
net_input=net_input+w3[i][j]*h2[i];
}
/* シグモイドの適用 */
y[j]=sigmoid(net_input);
printf("y > %lf (%d.%d.%d)\n",y[j],tx[isample][0],tx[isample][1],tx[isample][2]);
}
/* 逆方向の動作 */
/* 出力層の逆伝播 */
for(j=0;j<NUM_OUTPUT;j++){
y_back[j]=(y[j]-ty[isample][j])*((double)1.0-y[j])*y[j];
}
/* 隠れ層2の逆伝播 */
for(i=0;i<NUM_HIDDEN_TWO;i++){
net_input=0;
for(j=0;j<NUM_OUTPUT;j++){
net_input=net_input+w3[i][j]*y_back[j];
}
h2_back[i]=net_input*((double)1.0-h2[i])*h2[i];
}
/* 隠れ層1の逆伝播 */
for(i=0;i<NUM_HIDDEN_ONE;i++){
net_input=0;
for(j=0;j<NUM_HIDDEN_TWO;j++){
net_input=net_input+w2[i][j]*h2_back[j];
}
h1_back[i]=net_input*((double)1.0-h1[i])*h1[i];
}
/* 結合荷重の修正 */
for(i=0;i<NUM_INPUT+1;i++){
for(j=0;j<NUM_HIDDEN_ONE;j++){
w1[i][j]=(alpha*w1[i][j])-(epsilon*x[i]*h1_back[j]);
}
}
for(i=0;i<NUM_HIDDEN_ONE+1;i++){
for(j=0;j<NUM_HIDDEN_TWO;j++){
w2[i][j]=(alpha*w2[i][j])-(epsilon*h1[i]*h2_back[j]);
}
}
for(i=0;i<NUM_HIDDEN_TWO+1;i++){
for(j=0;j<NUM_OUTPUT;j++){
w3[i][j]=(alpha*w3[i][j])-(epsilon*h2[i]*y_back[j]);
}
}
}
}
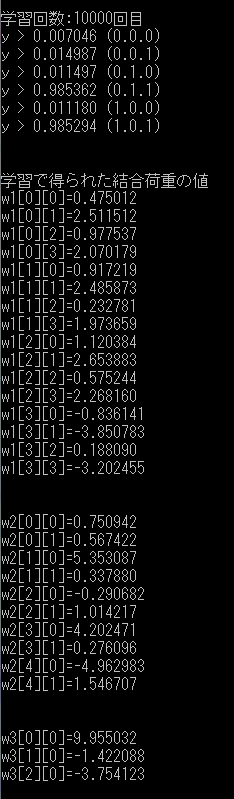
/* 学習後の結合荷重の値(この値をdeepfuture.cのプログラムに適用する事で論理回路の出力についての予測値を求める) */
printf("\n\n");
printf("学習で得られた結合荷重の値\n");
for(i=0;i<NUM_INPUT+1;i++){
for(j=0;j<NUM_HIDDEN_ONE;j++){
printf("w1[%d][%d]=%f\n",i,j,w1[i][j]);
}
}
printf("\n\n");
for(i=0;i<NUM_HIDDEN_ONE+1;i++){
for(j=0;j<NUM_HIDDEN_TWO;j++){
printf("w2[%d][%d]=%f\n",i,j,w2[i][j]);
}
}
printf("\n\n");
for(i=0;i<NUM_HIDDEN_TWO+1;i++){
for(j=0;j<NUM_OUTPUT;j++){
printf("w3[%d][%d]=%f\n",i,j,w3[i][j]);
}
}
return 0;
}
それではこのプログラムを用いて学習の方を行っていきます。結果は各自で変わると思いますが、おおむね次のような学習結果が得られるはずです。指定した学習回数の出力値が表1とほぼ同じなら学習は上手くいっています。学習が上手くいかない場合はもう一度プログラムを動かしてみてください。学習が成功したら学習で得られた結合荷重の値を使って論理回路の予測を行っていきます。
論理回路の予測
論理回路の予測ですが、学習で得られた結合荷重の値を使えば入力値を順方向に流すだけで予測値が得られます。そのためソースコードも学習の時とは違い、シンプルなものになっています。
/* プログラム名:deepfuture.c */
/* ディープラーニング(予測) */
# include<stdio.h>
# include<stdlib.h>
# include<math.h>
# include<time.h>
/* deeplearn.cで用いた入力層、中間層、出力層の値を設定する */
# define NUM_INPUT 3 /* 入力層の数(論理回路の入力)*/
# define NUM_HIDDEN_ONE 4 /* 中間層1の数(自由)*/
# define NUM_HIDDEN_TWO 2 /* 中間層2の数(自由)*/
# define NUM_OUTPUT 1 /* 出力層の数(論理回路の出力)*/
/* シグモイド関数 */
double sigmoid(double x){
double f;
f=1.0/(1.0+exp(-x));
return f; /* 戻す値が関数値 */
}
double x[NUM_INPUT+1],h1[NUM_HIDDEN_ONE+1],h2[NUM_HIDDEN_TWO+1],y[NUM_OUTPUT]; /* xが入力、h1が中間1、h2が中間2、yが出力 それぞれニューロンの値。+1は閾値表現用 */
int main(void){
int i,j;
double net_input;
/* deeplearn.cで得られた結合荷重の値をw1,w2,w3に設定する */
/* 今回の場合は次のような形で設定する事になる */
double w1[NUM_INPUT+1][NUM_HIDDEN_ONE]={{0.475012,2.511512,0.977537,2.070179},
{0.917219,2.485873,0.232781,1.973659},
{1.120384,2.653883,0.575244,2.268160},
{-0.836141,-3.850783,0.188090,-3.202455}};
double w2[NUM_HIDDEN_ONE+1][NUM_HIDDEN_TWO]={{0.750942,0.567422},
{5.353087,0.337880},
{-0.290682,1.014217},
{4.202471,0.276096},
{-4.962983,1.546707}};
double w3[NUM_HIDDEN_TWO+1][NUM_OUTPUT]={{9.955032},{-1.422088},{-3.754123}};
/* 予測値を求めるのに使う入力(この値を変更する事で予測値も変わる。今回の論理回路では予測に使う入力が2パターンあるため予測値を出したい入力をどちらか設定する) */
double tx[1][NUM_INPUT]={{1,1,0}};
printf("入力値\n");
for(i=0;i<1;i++){
for(j=0;j<NUM_INPUT;j++){
printf("x[%d]=%.01f\n",j,tx[i][j]);
}
}
printf("\n");
/* 順方向の動作 */
/* ネットワークへの入力設定 */
for(i=0;i<NUM_INPUT;i++){
x[i]=tx[0][i];
}
/* 閾値設定x */
x[NUM_INPUT]=(double)1.0;
/* 隠れ素子1の計算 */
for(j=0;j<NUM_HIDDEN_ONE;j++){
net_input=0;
for(i=0;i<NUM_INPUT+1;i++){
net_input=net_input+w1[i][j]*x[i];
}
/* シグモイドの適用 */
h1[j]=sigmoid(net_input);
}
/* 閾値設定h1 */
h1[NUM_HIDDEN_ONE]=(double)1.0;
/* 隠れ素子2の計算 */
for(j=0;j<NUM_HIDDEN_TWO;j++){
net_input=0;
for(i=0;i<NUM_HIDDEN_ONE+1;i++){
net_input=net_input+w2[i][j]*h1[i];
}
/* シグモイドの適用 */
h2[j]=sigmoid(net_input);
}
/* 閾値設定h2 */
h2[NUM_HIDDEN_TWO]=(double)1.0;
/* 出力素子の計算 */
for (j=0;j<NUM_OUTPUT;j++){
net_input=0;
for(i=0;i<NUM_HIDDEN_TWO+1;i++){
net_input=net_input+w3[i][j]*h2[i];
}
/* シグモイドの適用 */
y[j]=sigmoid(net_input);
printf("予測値\n");
printf("y > %.3lf\n",y[j]);
}
return 0;
}
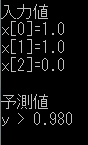
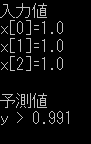
それではこのプログラムを用いて予測の方を行っていきます。予測に使う入力が2パターン(1,1,0と1,1,1)あるため、それぞれの入力値をソースコードに書いてプログラムを動かしてみた結果、次のような予測値が出てきました。
図4、図5と表1を比較すると図4は予測が上手くいっていますが、図5は間違っています。予測が上手くいかなかった原因としては中間層におけるニューロンの不足や過学習等が影響しているのでしょう。表2のパラメータを調節する事で両方を正しく予測する事が出来ますので、興味のある方はいろいろ試してみてください。
図4、図5と表1を比較すると図5の予測値が表1の出力値と異なっている事が分かると思います。実はNNもDLもパターン学習のアルゴリズムであるため、今回は1が多く入力されている時に1を出力するように学習をさせてしまいました。そのため、入力(1,1,1)の時に出力を0にするためにはそれに対応するような訓練データを用意しなければいけません。今回、用意した訓練データにそのデータを加えれば予測は上手くいくと思いますので興味のある方はいろいろ試してみてください。
むすび
今回はDLを使って論理回路を学習し、予測まで行ってみました。DLは研究盛んなアルゴリズムであるため、学習計算の仕方やパラメータ設定の方法など考える事は様々あります。本記事で紹介したプログラムはNNの層を1つ増やしただけのものとなっておりますので、これからDLについて勉強したいと思っている方は参考にしてもらえたら嬉しいです。