こんにちは。いしたーです。
今回はテイラー展開は何を意味しているのか、なぜ関数を多項式で近似できるのかを図を使って説明します。
テイラー展開は大学や高専の授業で習うと思います。関数 $f(x)$ の任意の $x$ に対する値を、 $f(x)$ の $a$ における値とその微分値 $(f(a), f'(a), f''(a), ....)$ を使って求められるというものです。
f(x) = \sum_{k=0} ^ {\infty} \frac {f^{(k)}(a)}{k!} (x-a)^{k}
この式をぱっと見て、なぜこれが成り立つかを理解するのは難しいと思います。少なくともこの式が何を意味しているのか、私はすぐには理解できませんでした。
端的に言うと、テイラー展開は
等加速度直線運動をしている物体のある時刻における位置と速度と加速度がわかれば、物体の$\Delta t$秒後の位置がわかる
ということを表しています。
ここでは、「等加速度運動をしている物体の距離を求める」という問題を眺めることで、テイラー展開を理解することを試みます。
2次のテイラー展開は等加速度直線運動の公式と同じ
まずは、テイラー展開と等加速度直線運動の公式が同じものであることを確認するため、2次のテイラー展開から等加速度直線運動の式を導いてみます。
テイラー展開は、和の記号 $\Sigma$ を外すと、
f(x) = f(a) + \frac {f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots
となりますよね。
$x-a$ を $h$ 、 $a$ を $x$ に置き換えてみると
f(x+h) = f(x) + \frac{f'(x)}{1!}h + \frac{f''(x)}{2!}h^2 + \frac{f'''(x)}{3!}h^3+ \cdots
となります。この式は
$x$ から $h$ だけ離れた場所での $f$ の値 $f(x+h)$ は、 $f(x)$ とその微分値を用いて表現できる
ということを意味しています。
もし $f(x)$ の2階微分が定数になるなら、3階微分以降の値は0になります。このときテイラー展開は次のように書くことができます。
f(x+h) = f(x) + \frac {f'(x)}{1!} h + \frac{f''(x)}{2!}h^2
等加速度直線運動の式に似せるため、ここでまた式を書き換えます。
$x$ を $t_0$ 、 $f$ を $x$ 、 $h$ を $\Delta t$ とすると、
\begin{align}
x(t_0+\Delta t)
&= x(t_0) + \frac{x'(t_0)}{1!}\Delta t + \frac{x''(t_0)}{2!}\Delta t^2 \\
&= x(t_0) + x'(t_0)\Delta t + \frac{x''(t_0)}{2}\Delta t^2
\end{align}
$v(t) := x'(t)$ 、 $a(t) := x''(t)$ とすると、
x(t_0+\Delta t) = x(t_0) + v(t_0)\Delta t + \frac{a(t_0)}{2}\Delta t^2
$t_0 = 0$ のとき、
x(\Delta t) = x(0) + v(0)\Delta t + \frac{a(0)}{2}\Delta t^2
等加速度直線運動の公式が出てきました。
上の式は
等加速度直線運動をしている物体の時刻 $t_0$ における位置と速度と加速度がわかれば、物体の $\Delta t$ 秒後の位置がわかる
ということを表しています。
つまり2次のテイラー展開は
定加速度運動をしている物体の時刻 $t_0$ における位置を $x(t_0)$ 、速度を $v(t_0)$ 、加速度を $a(t_0)$ とする。
この物体の $\Delta t$ 秒後の位置 $x(t_0+\Delta t)$ を求めなさい。
という問題を解いているのと同じだと言えます。
運動方程式からテイラー展開を導いてみる
運動方程式から2次のテイラー展開を求める
今度は逆に、先ほどの
定加速度運動をしている物体の時刻 $t_0$ における位置を $x(t_0)$ 、速度を $v(t_0)$ 、加速度を $a(t_0)$ とする。
この物体の $\Delta t$ 秒後の位置 $x(t_0+\Delta t)$ を求めなさい。
という問題を解くことによって、運動方程式から2次のテイラー展開を導いてみます。
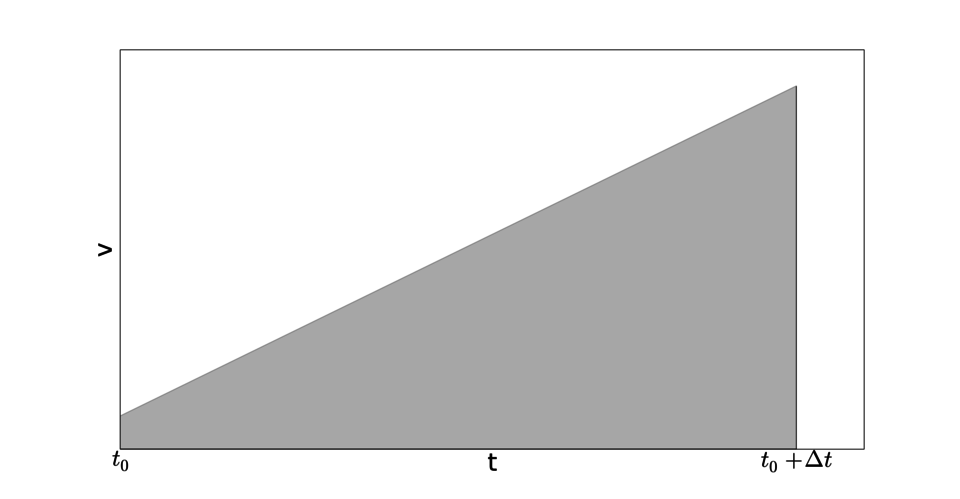
加速度 $a$ は定数なので、 $v-t$ グラフは一次関数になります。この $v-t$ グラフの面積が位置の変化量にあたるので、初期位置と変化量の和が $x(t_0+\Delta t)$ になります。
$v-t$ グラフを積分する過程で2次のテイラー展開が出現します。さっそくグラフを描いてみましょう。
このグラフの傾きが加速度 $a$ 、積分値が $\Delta t$ 秒間の位置の変化量 $x(t_0+\Delta t)-x(t_0)$ です。
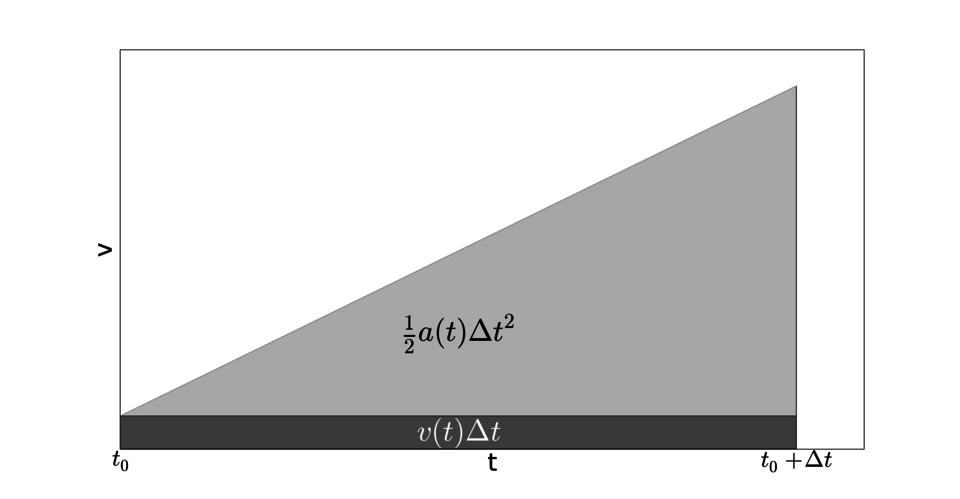
$v-t$ グラフを2つの部分に分割してみます。
上の三角形の部分は $\frac{1}{2}a(t_0) \Delta t^2$ 、下の部分は $v(t_0)\Delta t$ になっています。位置の変化量はこれらの和なので、
\begin{align}
x(t_0+\Delta t)-x(t_0) &= v(t_0)\Delta t + \frac{1}{2}a(t_0) \Delta t^2 \\
x(t_0+\Delta t) &= x(t_0) + v(t_0)\Delta t + \frac{1}{2}a(t_0) \Delta t^2
\end{align}
すなわち
x(t_0+\Delta t) = x(t_0) + x'(t_0)\Delta t +\frac{1}{2}x''(t_0) \Delta t^2
となります。この式は関数 $x(t)$ の2次のテイラー展開そのものですね。
3次のテイラー展開を求める
次は加速度の変化率が定数の場合を考えてみます。加速度の変化率は躍度と言い、一般的には $j$ で表すようです。
定躍度運動をしている物体の時刻 $t_0$ における位置を $x(t_0)$ 、速度を $v(t_0)$ 、加速度を $a(t_0)$ 、躍度を $j(t_0)$ とする。
この物体の $\Delta t$ 秒後の位置 $x(t_0+\Delta t)$ を求めなさい。
今度は躍度が定数なので、まず $a-t$ グラフを描き、それを2度積分することによって $x(t_0+\Delta t)$ を求めます。
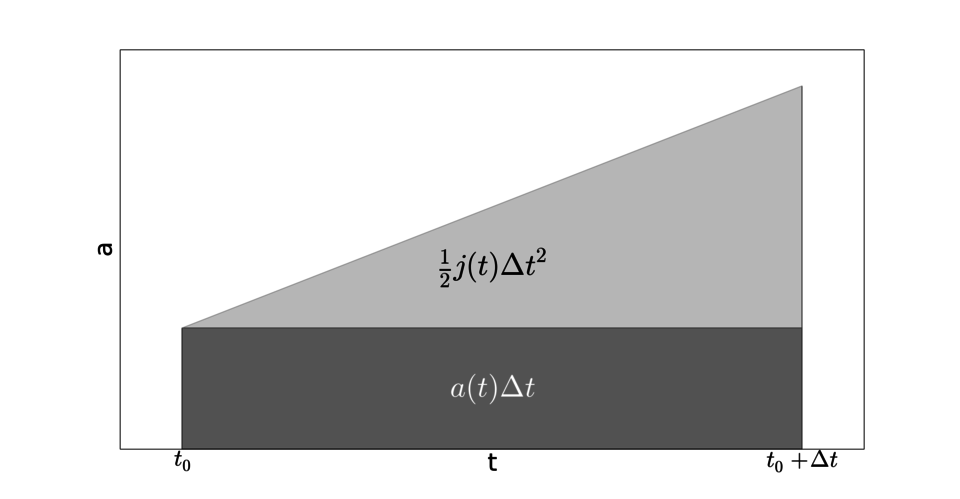
では $a-t$ グラフを描いてみます。
このグラフの面積は速度の変化量を表しています。
\begin{align}
v(t_0+\Delta t)-v(t_0) & = a(t_0)\Delta t + \frac{1}{2}j(t_0) \Delta t^2 \\
v(t_0+\Delta t) & = v(t_0) + a(t_0)\Delta t + \frac{1}{2}j(t_0) \Delta t^2 \\
\end{align}
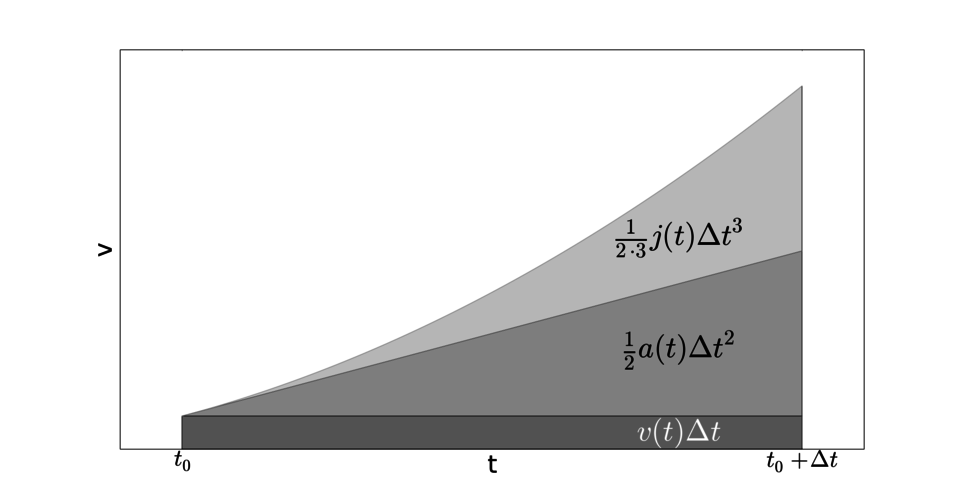
$v-t$ グラフを描いてみます。
$v-t$ グラフの面積が位置の変化量にあたるので、先ほどと同様に
\begin{align}
x(t_0+\Delta t)-x(t_0) & = v(t_0)\Delta t + \frac{1}{2}a(t_0) \Delta t^2 + \frac{1}{2 \cdot 3}j(t_0) \Delta t^3\\
x(t_0+\Delta t) & = x(t_0) + v(t_0)\Delta t + \frac{1}{2}a(t_0) \Delta t^2 + \frac{1}{2 \cdot 3}j(t_0) \Delta t^3
\end{align}
となるので、
x(t_0+\Delta t) = x(t_0) + x'(t_0)\Delta t + \frac{1}{2}x''(t_0) \Delta t^2 + \frac{1}{2 \cdot 3}x'''(t_0) \Delta t^3
3次のテイラー展開が出てきました。
n次のテイラー展開
3次のテイラー展開の導出までお見せしましたが、4次のテイラー展開でも話は同じです。
4次の場合は傾きが一定の $j-t$ グラフを描き、それを3度積分すれば先ほどと同じようにテイラー展開を導くことができます。
先ほどの $v-t$ グラフを見ていただければわかるとおり、 $x^{(n)}(t_0)$ によって生じる $x$ の変化量は $\frac{1}{n!}x^{(n)}(t_0)\Delta t^n$ です。
このことから、
$x^{(n)}(t_0)$ は $x$ を $\Delta t$ 秒後に $\frac{1}{n!}x^{(n)}(t_0)\Delta t^n$ だけ増加させる
ということがわかります。
n次のテイラー展開の $v-t$ グラフを見ると、それぞれの導関数に起因する $x$ の変化量
x'(t_0)\Delta t,\hspace{1em} \frac{1}{2}x''(t_0)\Delta t^2,\hspace{1em} \frac{1}{2 \cdot 3}x'''(t_0)\Delta t^3, \dots,\hspace{1em} \frac{1}{n!}x^{(n)}(t_0)\Delta t^n
の総和がxの最終的な増加量になります。
例えば3次のテイラー展開の場合はこうです。
x(t_0+\Delta t) - x(t_0) = x'(t_0)\Delta t + \frac{1}{2}x''(t_0)\Delta t^2 + \frac{1}{2 \cdot 3}x'''(t_0)\Delta t^3
n次の場合はこうです。
\begin{align}
x(t_0+\Delta t) - x(t_0) &= x'(t_0)\Delta t + \frac{1}{2}x''(t_0)\Delta t^2 + \frac{1}{2 \cdot 3}x'''(t_0)\Delta t^3 + ... + \frac{1}{n!}x^{(n)}(t_0)\Delta t^n \\
x(t_0+\Delta t) &= x(t_0) + x'(t_0)\Delta t + \frac{1}{2}x''(t_0)\Delta t^2 + \frac{1}{2 \cdot 3}x'''(t_0)\Delta t^3 + ... + \frac{1}{n!}x^{(n)}(t_0)\Delta t^n
\end{align}
和の記号を使って書き直すと
x(t_0+\Delta t) = \sum_{k=0}^n \frac{1}{k!}x^{(k)}(t_0)\Delta t^k
となり、n階微分が定数となる関数 $x(t)$ のテイラー展開を導くことができました。
おわりに
できるだけわかりやすく書こうと試みてはいるものの、数式が多いため読みにくくなってしまっている部分があると思います。
「こう書いたらもっとわかりやすい」という意見があればコメント欄に書いていただけると嬉しいです。