はじめに
代表的なクラスタリングアルゴリズムである K-Means を用いて、画像の圧縮をしてみます。まずは、K-Means のアルゴリズムについて説明します。そのあと、K-Meansを使った画像圧縮について説明します。なお、内容についてはCoursera Machine Learningを参考にしています。
クラスタリングとは?
データの集まりをデータ間の類似度に従って、いくつかのグループ(クラスタ)に分けること。
K-Means アルゴリズム
アルゴリズムの直感的な説明
K-Means アルゴリズムは大きく分けて以下の3つの処理に分解されます:
- 重心の初期化
- クラスタ割り当て
- 重心の再計算
それぞれのステップについて、イメージを交えて理解していきましょう。
1. 重心の初期化
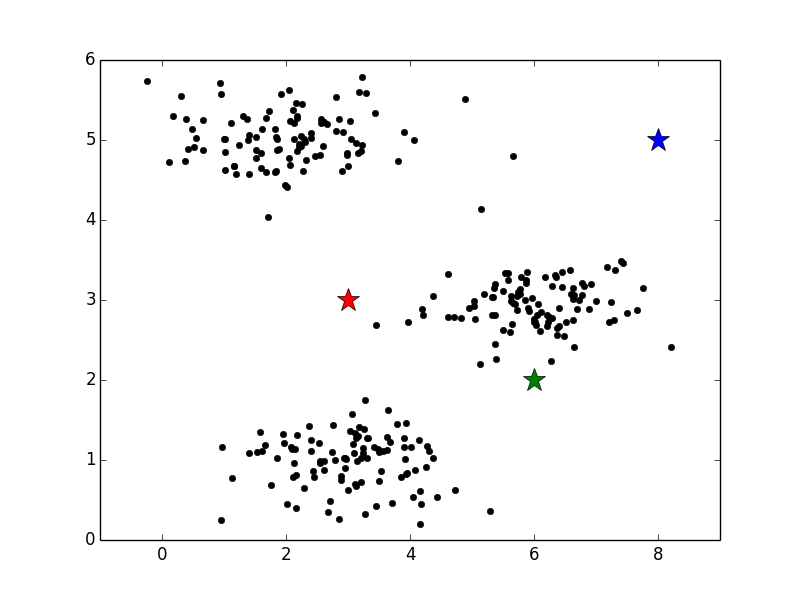
まずは、重心と呼ばれる点の位置を決定します。それぞれの重心は各クラスタの標準的なパターンとみなされます。そのためデータを分けたいクラスタ数分の重心が必要です。下図では星印が重心、丸印がデータを表しています。ここでは重心の数は3つなので、データを赤、青、緑3つのクラスタに分けることになります。
この図では、ランダムに重心を決定していますが、後ほど別の方法を紹介します。
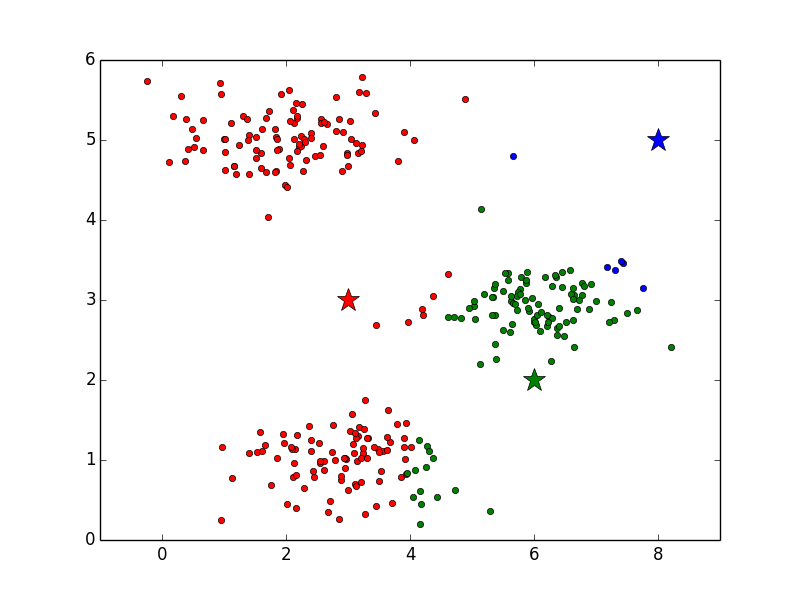
2. クラスタ割り当て
重心の位置を決定したら、次は各データにクラスタを割り当てます。ここでは、各データを見て行って、赤、青、緑のクラスタ重心のどれと近いかによって、データをいずれかのクラスタに割り当てます。
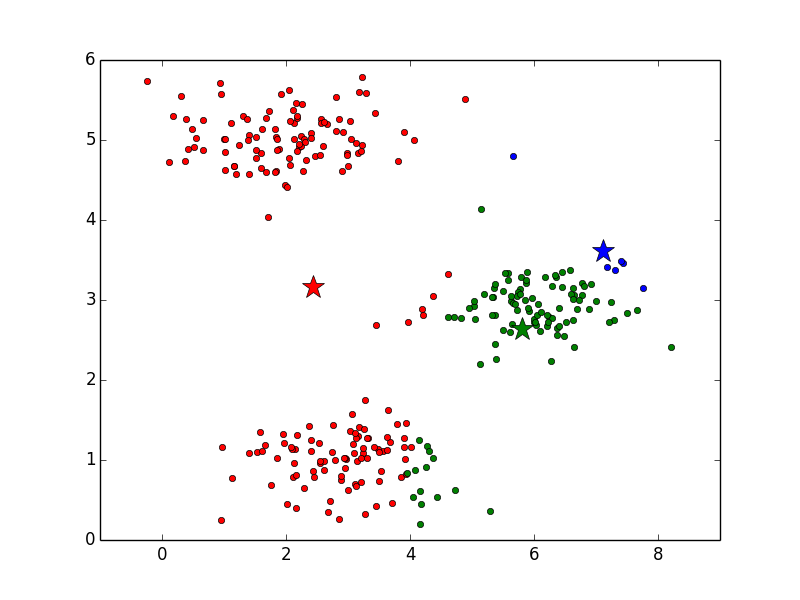
3. 重心の再計算
全データへのクラスタの割り当てが終わったら、重心の位置を再計算します。このとき、各クラスタ内のデータの平均値を新たな重心の位置とします。たとえば、緑の重心を計算する場合は、緑の丸印をすべて足し合わせて、その個数で割ることで重心を求めます。上図と下図を比べると、重心の位置が変化していることが確認できると思います。特に青と緑が動いていることがわかりやすいと思います。
4. 2と3の繰り返し
以降はクラスタ割り当てと重心の再計算を繰り返し実行します。その様子は以下のアニメーションで確認できます。ここで、重心の色は見やすくするために黒にしています。最後の方では収束して重心の位置が変化していないことがわかります。
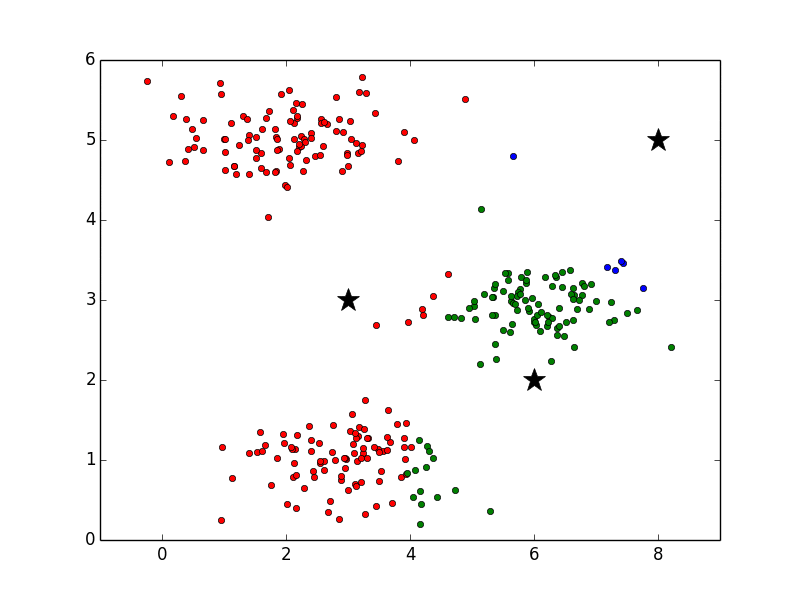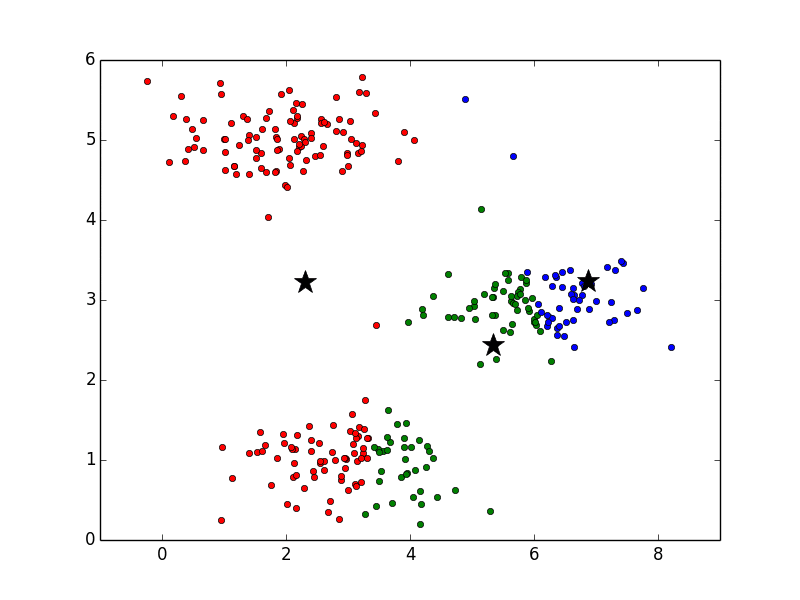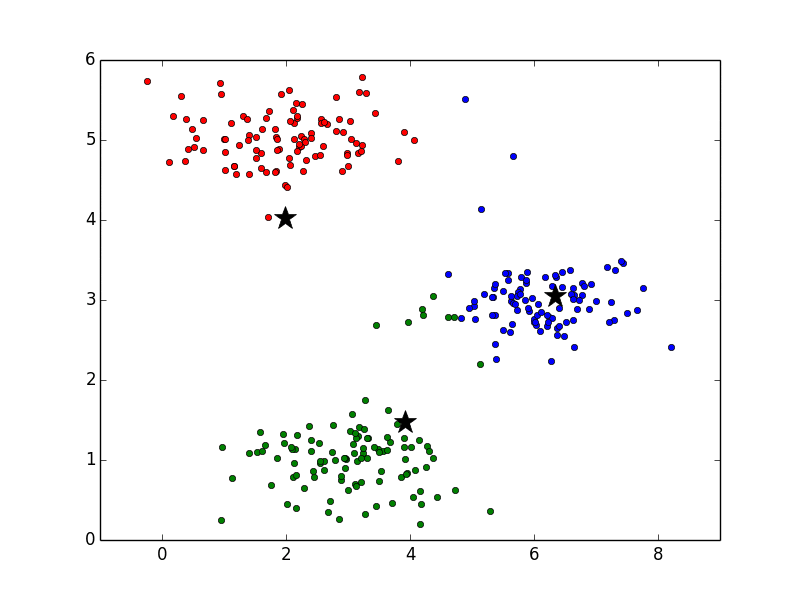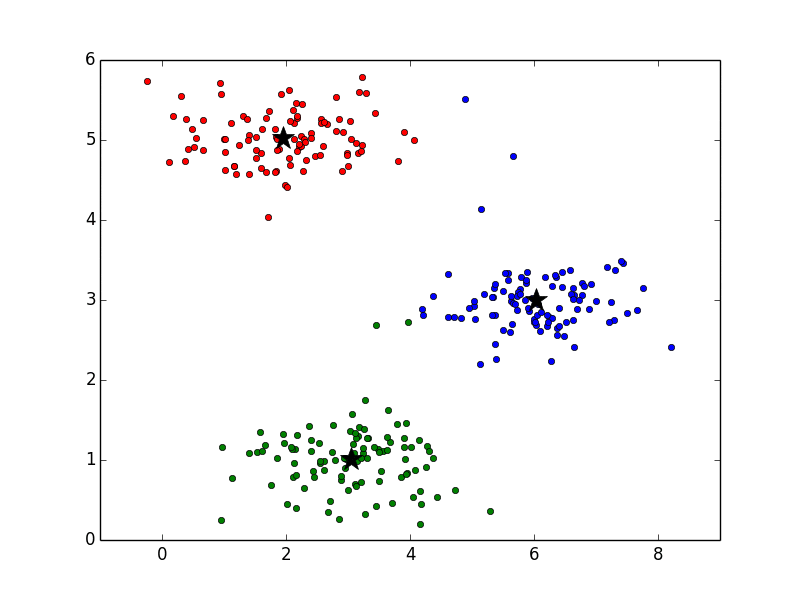
また、重心は静止画で見ると以下のような軌跡で動いていることがわかります。
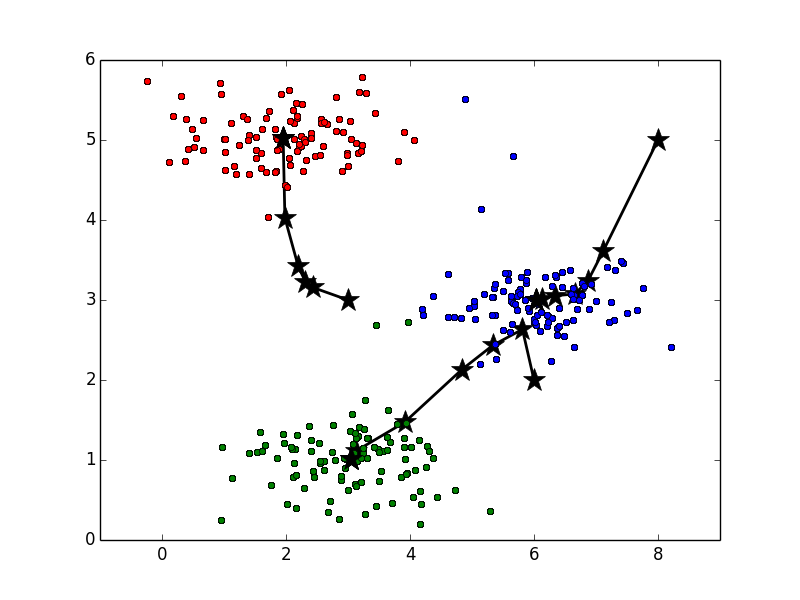
アルゴリズムの形式化
以上で説明した K-Means アルゴリズムをコードにまとめると以下のようになります。
# 重心の初期化ステップ
centroids = kmeans_init_centroids(X, K)
for iter in range(iterations):
# クラスタ割り当てのステップ: 各データに最も近い重心が属するクラスタを割り当てる。
# idxはリストで、idx[i]にはi番目のデータに割り当てられた重心のインデックスが格納されている
idx = find_closest_centroids(X, centroids)
# 重心移動ステップ: 重心割り当てに基づいたクラスタ内の平均を計算
centroids = compute_centroids(X, idx, K)
アルゴリズムへの入力は以下の2つです。
- クラスタ数 $K$
- トレーニングセット { $x^{(1)}, x^{(2)},...,x^{(m)}$ } , $x^{(i)} \in \mathbb{R}^n$
K-Means は教師なし学習なので、トレーニングセットにはラベルは付いていません。各トレーニングデータ $x^{(i)}$ は $n$次元のベクトルとなります。それぞれ図の丸印に対応しています。また、クラスタ数は事前に決定しておく必要があります。
入力データもわかったところで、アルゴリズムの各ステップについて説明していきます。
重心の初期化
最初に重心の初期化を行います。重心は $u^{(j)}$ で表される $n$次元のベクトルで、$K$個存在します。図では星印の点に対応しています。
u^{(1)}, u^{(2)},...,u^{(K)} \in \mathbb{R}^n
重心の初期化の方法としては、トレーニングセット $x^{(1)}, x^{(2)},...,x^{(m)} \in \mathbb{R}^n$ からランダムに $K$個選択する方法があります。具体的には、トレーニングセットをランダムにシャッフルした後、最初の $K$個を重心として選択します。
コードとして実装すると以下のようになります。
from numpy import *
def kmeans_init_centroids(X, K):
# 重心がランダムなデータになるように初期化する
# トレーニングデータをランダムに並び替える
rand_X = random.permutation(X)
# 最初のK個を重心として採用する
centroids = rand_X[:K]
return centroids
クラスタ割り当て
重心の初期化が終わったら、各データにクラスタを割り当てます。具体的には、各トレーニングデータ $x^{(i)}$ に最も近い重心 $u_j$ を探し、その重心のクラスタを割り当てます。
データに最も近い重心の探索では、以下のようにして距離の二乗を求めます。距離の二乗が最小となる重心のクラスタを割り当てます。
idx^{(i)} := argmin_j ||x^{(i)} − μ_j||^2
ここで $idx^{(i)}$ は $x^{(i)}$ に最も近い重心のインデックスであり、$u_j$は $j$番目の重心の座標です。
numpyを使って素朴に実装すると以下のようになります。
import sys
from numpy import *
def find_closest_centroids(X, centroids):
K = centroids.shape[0]
m = X.shape[0]
idx = zeros((m, 1))
for i in range(m):
lowest = sys.maxint
lowest_index = 0
for j in range(K):
cost = X[i] - centroids[j]
cost = cost.T.dot(cost)
if cost < lowest:
lowest_index = j
lowest = cost
idx[i] = lowest_index
return idx
scipy の scipy.spatial.distance.cdist を使うと以下のように短く書けます。cdist には様々な距離の計算方法が定義されています。その中でも、今回は二乗距離を使用しました。パフォーマンスも上の素朴なコードよりこちらの方が良いです。
import scipy.spatial.distance
from numpy import *
def find_closest_centroids(X, centroids):
sqdists = scipy.spatial.distance.cdist(centroids, X, 'sqeuclidean') # 二乗距離を求める
idx = argmin(sqdists, axis=0) # 各データに対する最も近い重心のインデックス
return idx
重心の再計算
データのクラスタへの割り当てが終わったら、重心を再計算します。
すべてのデータがあるクラスタに割り当てられたら、次に行うのは重心の再計算です。ここでは、クラスタに割り当てられたデータの平均を計算します。すべての重心 $k$ に対して、以下の式を実行します。
u_k := \frac{1}{|C_k|} \sum_{i \in C_k} x^{(i)}
ここで $C_k$ は重心 $k$ が割り当てられたデータ集合です。具体的には、もし2つのデータ $x^{(3)}$ と $x^{(5)}$ が重心 $k=2$ に割り当てられたら、$u_2=\frac{1}{2}(x^{(3)} + x^{(5)})$ になります。
素朴に実装すると以下のようになります。
from numpy import *
def compute_centroids(X, idx, K):
m, n = X.shape
centroids = zeros((K, n))
for k in range(K):
temp = X[idx == k] # クラスタkに割り当てられたデータを取り出す
count = temp.shape[0] # クラスタkに割り当てられたデータ数
for j in range(n):
centroids[k, j] = sum(temp[:, j]) / count
return centroids
numpy の mean関数を使って短く書くとこんな感じになります。
from numpy import *
def compute_centroids(X, idx, K):
m, n = X.shape
centroids = zeros((K, n))
for k in range(K):
centroids[k] = mean(X[idx == k], axis=0)
return centroids
画像圧縮
概要
さて、アルゴリズムの説明が終わったところで本題の画像圧縮に話は移ります。
K-Meansアルゴリズムを応用することで、画像の圧縮を行うこともできます。ざっくり説明すると、K-Meansを用いて圧縮画像を表すのに使う $K$色を選択します。この $K$色で元画像のピクセルを置き換えることで、圧縮を行います。以下では $K=16$として説明していきます。
色の表現方法
もし画像のピクセルが 24bitの色表現なら、3つの 8bit表現に分解できます。それぞれの 8bitが赤、青、緑に対応するもので、いわゆる RGB です。8bitなのでそれぞれ0〜255( $2^0〜2^8 - 1$ )の値を取ることができます。そんなわけで、これらの値の組み合わせによって画像は無数の色を含むわけですが、ここではその色数を $K = 16$色まで減らします。16色まで色数を減らすことで、各ピクセルを4bitで表現できるようになるはずです。( $16 = 2^4$ )
下の図では、左の画像中に含まれる各ピクセルのRGB値を3次元空間上に写像すると右の画像になることを示しています。
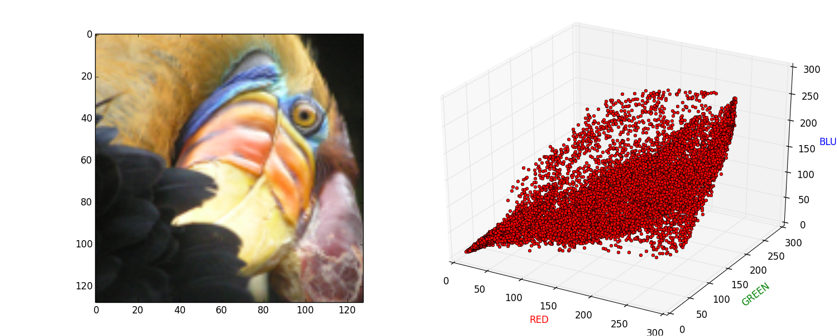
K-Means の適用
K-Meansアルゴリズムを用いることで、圧縮画像を表すのに使われる16色を選択します。具体的には、元画像の各ピクセルをデータとして入力し、K-Meansアルゴリズムを用いて16色のグループにクラスタリングします。一旦重心を計算すれば、元画像のピクセルのRGB値をその重心のRGB値に置き換えることで、画像を16色で表すことが可能になります。
イメージとしては以下の図のようになります。以下の図では星印が重心、丸印が各ピクセルを表しており、同じクラスタに属するピクセルは同じ色になっています。このとき、同じクラスタに属するピクセルの値をそのクラスタの重心の値で置き換えてしまいます。画像で言えば、同じ色の丸印の値をクラスタ重心の値に集約してしまうイメージです。なお計算の都合上、RGBの値は 0.0〜1.0 に変換してあります。
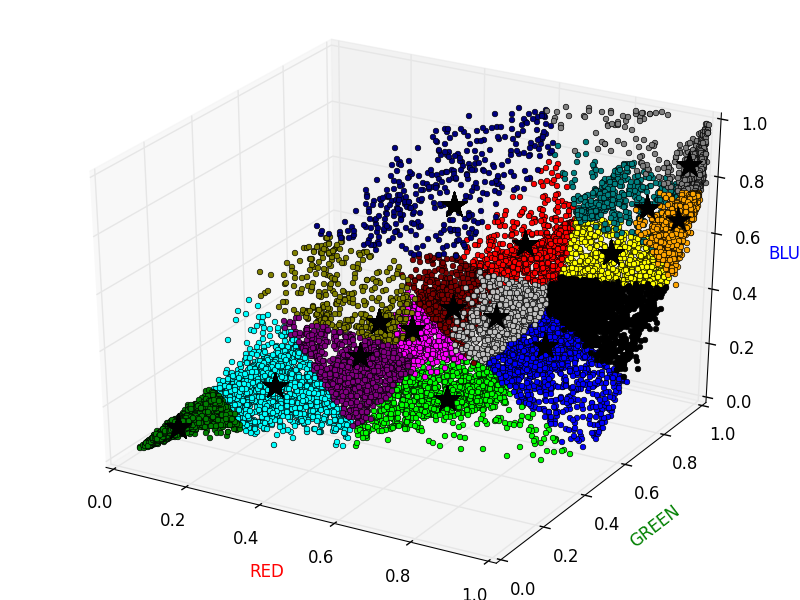
以下のアニメーションは、実際にK-Meansを画像に適用している様子です。クラスタの割り当てと重心の再計算を繰り返し行っていることがわかります。
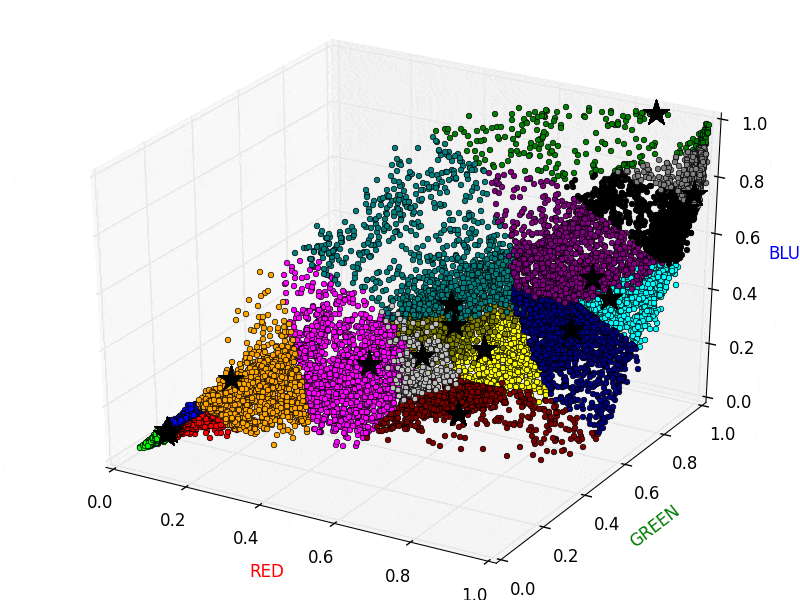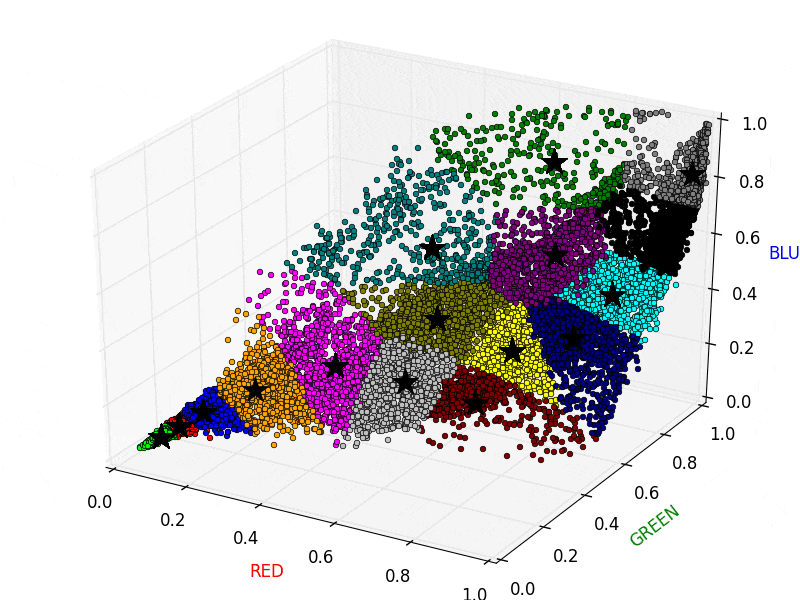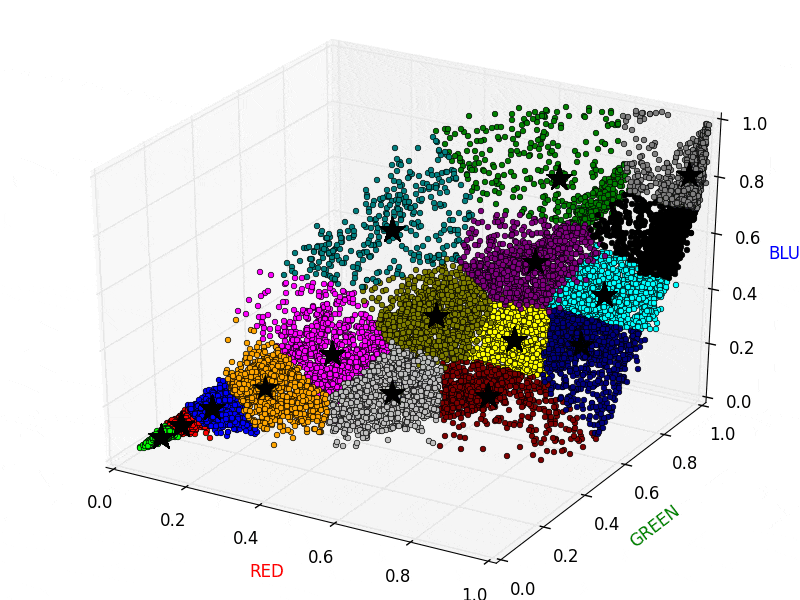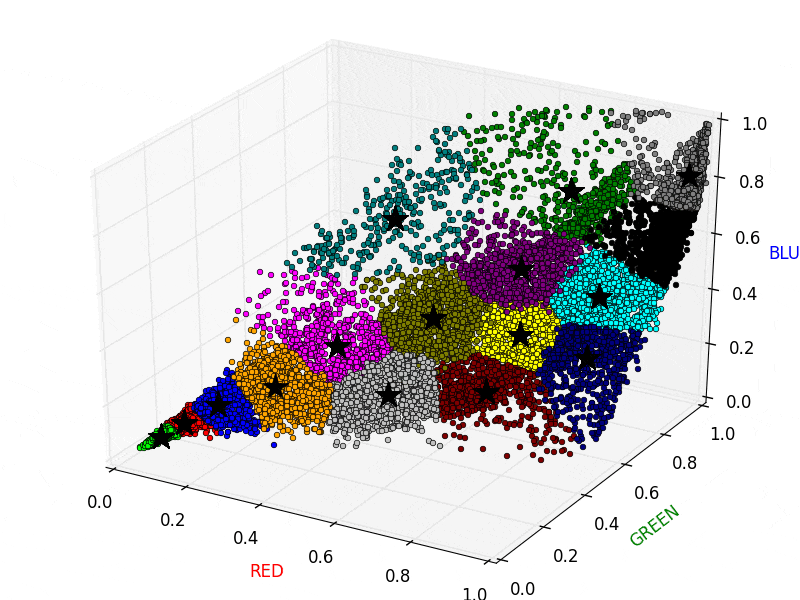
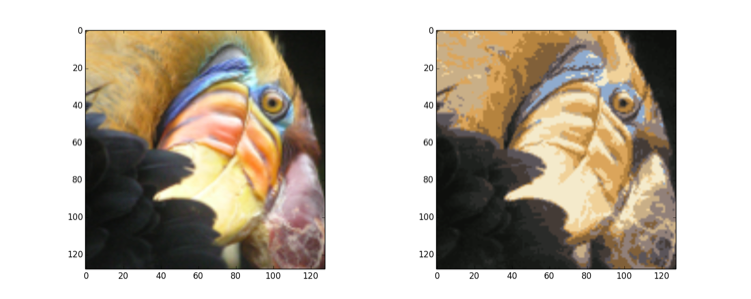
実際にK-Meansを適用した元画像と圧縮された画像です。左が元画像、右が圧縮された画像です。圧縮された画像は、色数が減って粗い表現になっていることが確認できます。
圧縮サイズ
画像を表す代表的な16色が見つかったら、各ピクセルの値を最も近い重心の値で置き換えてしまいます。これは元画像を各ピクセルに割り当てられた重心で表現することに相当します。重心の数は16しかないので、画像を表すのに必要なビット数が大幅に減ることになります。元画像と圧縮画像に必要なbit数を見てみましょう。
今回用いた元画像はサイズが128 x 128ピクセルです。その各ピクセルにつき24bitの情報が必要でした。その結果としてトータルでは
128 x 128 x 24 = 393216 bit
が必要でした。
圧縮した画像では16色の情報を格納しておく分のbit数が必要です。また各色は24bitが必要ですが、画像そのものは1ピクセルにつき4bitしか必要としません。4bitで16色のうちのどの色を使うかを示せばいいからです。その結果、最終的には
16 x 24 + 128 x 128 x 4 = 65920 bit
で済むようになります。これはだいたい元画像の6分の1のサイズです。
サンプルコード
おわりに
今回は、K-Meansアルゴリズムを使って画像の圧縮をしてみました。圧縮結果の画像はイマイチですが、適用範囲の広いアルゴリズムだと思います。サンプルコードと合わせて是非一度動かしてみてください。