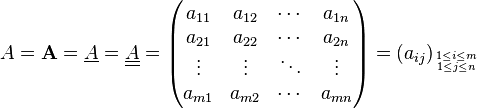目的
このシリーズは中学三年生程度の数学の知識があれば、Python言語の機械学習記述用ライブラリを利用して記述された、基本的な教師あり学習のニューラルネットワークである誤差伝搬型3層ニューラルネットワークのプログラム、つまり、TensorFlowのサイト(TensorFlow.org)上にあるTutorialのMNIST For ML Beginnersの内容をを理解できるということを目的としています
テンソルとは何か
早速本題に入り、まずはテンソルということについて考えて行きます
ベクトルとスカラー
テンソルについて説明する前に、まず、スカラーとベクトルについて説明します
スカラーとは大きさです。例えば距離、例えば重さ、そういうものを数学用語でスカラーといいます
ベクトルとは大きさと向きがあるものです。座標というものベクトルで考えることができます。それは原点をどこかにとれば、座標への向きと大きさが決まるからです
ところで実は、スカラーもベクトルもテンソルというものに属しているのです。テンソルとその階数という概念を使えばスカラーを0階のテンソルといい、ベクトルを1階のテンソルといいます
一般的なテンソルの定義をWikipedia ( https://ja.wikipedia.org/wiki/テンソル空間 )から引用すると、
共通の体 F 上のベクトル空間の有限集合 {V1, …, Vn} が与えられたとき、それらのテンソル積 V1 ⊗ … ⊗ Vn はふたたび F 上のベクトル空間であり、またその元はテンソルと呼ばれる。特に一種類のベクトル空間 V から作られるテンソル積空間
V\otimes \cdots \otimes V\otimes V'\otimes \cdots \otimes V' (式1)
を V 上のテンソル空間と呼び[2]、その元(ベクトル)をベクトル空間 V 上のテンソルと言う。ここに V∗ は V の双対空間である。
とあります。難しいですね。上の引用の要旨を挙げれば、「テンソル積というものが定義できるようなベクトル空間の元をテンソルと言う」、となるかと思います
テンソル積について
では、以下テンソル積ということについてもう少し考えてみたいと思います
例えば、$(x_0,y_0)$、$(x_1,y_1)$というものをベクトルa,bとみなして、直積というものをとるということを考えていきます
まず、ベクトルa,bは
a = $x_0$ ex + $y_0$ ey
b = $x_1$ ex + $y_1$ ey
とおけます。ここでex,eyはそれぞれ大きさ1のベクトル(単位ベクトル)で、x方向のy方向の向きを決定してしており、かつ直交(言うなれば垂直に交わっている)していると思って下さい。このような二つの単位ベクトルは平面というものを規定していたりしますので、難しい言い方では正規直交基底とも言います
どうしてベクトルをa = $x_0$ ex + $y_0$ ey のような数式で表すかというと、ベクトルexを$x_0$倍したものを一つのベクトルと見なしたときにその先端からベクトルeyを$y_0$倍したものを描くとちょうどその先端が座標$(x_0,y_0)$の地点を示しているからと考えてもらえば良いと思います
さて、ベクトルの積(直積)の記号を∧と書くことにします。すると、a,bの積(直積)は
a∧b = ($x_0$ ex + $y_0$ ey)∧($x_1$ ex + $y_1$ ey)
=$x_0$$x_1$ ex∧ex+$x_0$$y_1$ ex∧ey+$x_1$$y_0$ ey∧ex+$y_0$$y_1$ ey∧ey (式2)
と定義されることになります
(参考:高校生のための微分幾何 (differential geometry for dilettantes) とても良いサイトなので高校生以上の方は是非読んで見て下さい)
いま、ベクトルの直積ex∧eyとey∧exは異なると考えれば、直積の組み合わせは4通りとなります。(ただし、直積をウエッジ積同等と考えるならば場合ex∧ey=-ey∧exであるため基底としては3通り)
ここで、「高校生のための微分幾何 」から引用すれば、
2つのベクトル空間V,Wをとる。dim V=n、dim W=mとする。まず、VとWの基底を、それぞれ
V:{e1, e2, e3, ..... , en}
W:{f1, f2, f3, ..... , fm}
ととる。
テンソル積(空間)V⊗Wとは、基底として
VW:{e1⊗f1, e1⊗f2, ..... , e1⊗fm, e2⊗f1, ..... , e2⊗fm, e3⊗f1, ..... , ..... , en⊗fm}
をとるnm次元ベクトル空間であり、その元は、直積(a,b)(a∈V,b∈W)からc∈VWへの、次のような写像によって与えられる。
a = $a_1$ e1 + $a_2$ e2 + $a_3$ e3 + $a_4$ e4 + ... + $a_n$ en
b = $b_1$ f1 + $b_2$ f2 + $b_3$ f3 + $b_4$ f4 + ... + $b_m$ fm
として、(a,b) ├→ $Σa_i$$b_j$ ei⊗fj
この定義では、テンソル積とは空間の積であって、元の積ではないことに注意。
となっています。これはつまり、式2を、
a⊗b = $x_0$$x_1$ ex∧ex + $x_0$$y_1$ ex∧ey + $x_1$$y_0$ ey∧ex + $y_0$$y_1$ ey∧ey (式2')
と表すことができるという意味になります。では、この直積、例えば、ex∧eyとは何かが問題ですが、これは写像の際にあたらしく作られた基底であるということになります。
少しはテンソル積というもののイメージがつかめたでしょうか。
難しいテンソル空間の定義はこのくらいにしておこうと思います。
2階のテンソル
一般に2階のテンソルは行列で表せます。つまり、
のような形ですね(引用元:https://ja.wikipedia.org/wiki/行列 )
3階のテンソルとは、このようなm×n型の行列が例えばl個あるようなもの、4階のテンソルとは、m×nの行列l個がさらにk個あるとイメージすれば良いと思います
今回は非常に難解なテンソルについてお話しさせて頂きました。次回からはもう少し具体的な話をさせて頂きたいと思います