【プログラマーのための数学】一次結合 (線型結合)

目次

プログラマーのための数学 - 目次

一次結合とは

線型結合と呼ばれることもあります。
数式的意味と、空間的意味の2つで説明します。

数式的意味

Σ[i=1 to n] k[i]v[i] = k1v1→ + k2v2→+ ··· +knvn→

このように幾つかのベクトルの定数倍の和で表されるものをこれらのベクトルの１次結合という。

     | 1 |　　     |  1 |
v1 = | 0 |　　v2 = | -1 |
     | 0 |　　     |  0 |

このようなv1、v2という2つのベクトルがあるとき、

     |  5 |
v3 = | -3 |
     |  0 |

v3は、v1、v2の一次結合になります。

     |  5 |
v3 = | -3 | = k1v1 + k2v2
     |  0 |

k1=2、k2=3と値を代入することで、この式を成り立たせることができます。
このとき、v3は、v1、v2の一時結合ということになります。

しかし、もしv3が下記の場合は、v1、v2の一次結合にはなりません。

     | 0 |
v3 = | 0 |
     | 1 |

下記の式が成り立たないからです。

     | 0 |                   | 1 |     |  1 |   | 0 |
v3 = | 0 | = k1v1 + k2v2 = k1| 0 | + k2| -1 | = | 0 |
     | 1 |                   | 0 |     |  0 |   | 1 |

この式を満たすk1、k2は存在しません。
このとき、v3は、v1、v2の一次結合ではありません。

空間的意味

図で表すとこのようになります。

一次結合の場合

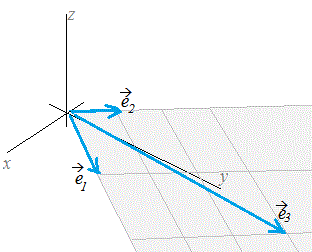
出典：http://www.geisya.or.jp/~mwm48961/linear_algebra/independent1.htm

     | 1 |　　     |  1 |       |  5 |
e1 = | 0 |　　e2 = | -1 |  e3 = | -3 |
     | 0 |　　     |  0 |       |  0 |

この場合、e3は、e1、e2が作る平面の上にあります。
e3は、e1、e2の一次結合となります。

一次結合ではない場合

出典：http://www.geisya.or.jp/~mwm48961/linear_algebra/independent1.htm

     | 1 |　　     |  1 |       | 0 |
e1 = | 0 |　　e2 = | -1 |  e3 = | 0 |
     | 0 |　　     |  0 |       | 1 |

この場合、e3は、e1、e2が作る平面の上にありません。
e3は、e1、e2の一次結合ではありません。

[参考]
www.geisya.or.jp
proofcafe.org

[関連記事]
プログラマーのための数学 - 目次