目次
ベクトルとは
ベクトルとは、向きと大きさを持ったものである。
位置に依存はしないので、向きと大きさが等しければ、そのベクトル同士は等しいということになる。
余談
日常会話の中で、「ベクトルが等しい」という表現が使われることがあるが、
大抵の場合は、「方向性が等しい」という意味で使用されている。
しかし、上記で述べた通り、ベクトルとは、方向だけでなく、大きさの2つを持っているので、
数学でいうと、方向性が同じでも大きさが異なれば、それは違うベクトルである。
ベクトルの演算
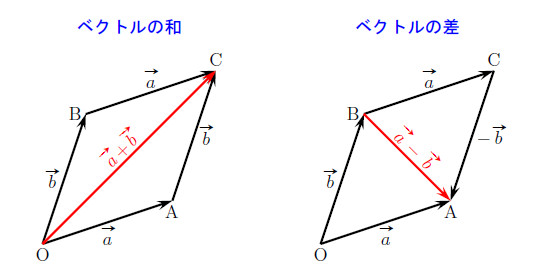
出典:受験の月
上図のような平行四辺形があるとき、下記の和、差が成り立つ。
- ベクトルの和
OC→ = OA→ + AC→
足し算は、2つのベクトルの終点と始点を合わせる。
OA→の終点と、AC→の始点を合わせる。
ベクトルの始点と始点をあわせる考え方の場合はOA→ + OB→となり、これでも同等の解になる。
ただ、個人的に、足し算は終点と始点をあわせるほうがイメージしやすい気がする。
- ベクトルの差
BA→ = OA→ + (-OB→)
引き算は、2つのベクトルの始点と始点を合わせる。
OA→の始点と、OB→の始点を合わせる。
ベクトルの差は、マイナスの足し算として捉えたほうが理解しやすい。
こちらも、OA→の終点と、AC→の始点を合わせる考え方もできるが、引き算は、始点と始点をあわせるほうがイメージしやすいと思う。
絶対値について
数学には絶対値という概念があり、簡単に言えば、向きを無視した大きさだけを表すものです。
最初に書いた通り、ベクトルとは向きを持っているので、
CA→とAC→は等しくない。CA→ = -OB→であり、AC→ = OB→である。
しかし、これらを絶対値で比較すると向きが関係なくなるので、すべて等しくなる。
|は絶対値であることを示す数学の記号。
|CA| = |AC| = |OB| = |BO|
[参考]
受験の月
[関連記事]
プログラマーのための数学 - 目次