目次
概要
数値データがあるときに、そのデータを代表する値のことを、代表値といいます。
代表値には、以下の3つがあります。データの分布の形によって、どれを代表値とするかが変わります。
- 平均値
- 中央値(メディアン)
- 最頻値(モード)
平均値
平均値とは、全てのデータの合計値を、データの数で割ったものです。
\bar{x} = \frac{(x_1+x_2+x_3+・・・+x_n)}{n}
度数分布表の場合は、「階級値」と「度数」を使って平均値を出すことができます。
n個の階級を持ち、階級値を v 、度数を f とすると、以下の式で算出することができます。
\bar{X} = \frac{(f_1v_1 + f_2v_2+ ・・・ + f_3v_3)}{(f_1 + f_2 + ・・・ + f_n)}
例として、10人の生徒のテストの点数の度数分布表を元に、平均値を出してみます。
| 階級 | 階級値 | 度数 |
|---|---|---|
| 0点以上25点未満 | 12.5 | 1 |
| 25点以上50点未満 | 37.5 | 3 |
| 50点以上75点未満 | 62.5 | 4 |
| 75点以上 | 87.5 | 2 |
このテストの点数の平均値は、以下で求められます。
\bar{X}=\frac{({1\times12.5}) + ({3\times37.5}) + ({4\times62.5}) + ({2\times87.5})}{(1+3+4+2)}
ちなみに、ちょっと話は逸れますが、平均値の算出方法というのは、用途によって複数あります。
こちらも参考にしてみてください。
関連記事:平均値の算出方法は1つじゃない
中央値(メディアン)
中央値とは、データを小さい順、もしくは大きい順で並べた時に、真ん中となる値のことです。データ数が偶数の場合は、中央値が2つとなり、それらを足して2で割ったものが中央値になります。
データ個数が奇数の場合
1, 3, 4, 5, 7
この場合は、中央値は 4 になります。
データ個数が偶数の場合
1, 3, 4, 5, 7, 10
この場合の中央値は 4 と 5 の2つになるので、以下の式で求められ、中央値は 4.5 となります。
4.5 = \frac{4+5}{2}
最頻値(モード)
最頻値とは、最もデータ数の多い値のことを指します。
1, 3, 4, 5, 7, 7, 10
例えば、上記の場合の最頻値は、7 となります。
度数分布表の場合は、最も度数が大きいものの階級値が、最頻値となります。
先ほどのテストの点数の度数分布表の場合、度数が一番大きいものは、「50点以上75点未満」の 4 となるので、最頻値はその階級値である 62.5 となります。
| 階級 | 階級値 | 度数 |
|---|---|---|
| 0点以上25点未満 | 12.5 | 1 |
| 25点以上50点未満 | 37.5 | 3 |
| 50点以上75点未満 | 62.5 | 4 |
| 75点以上 | 87.5 | 2 |
また、以下のように、 5 と 7 が同じ数だけある場合は、最頻値は 5 と 7 の2つになります。
1, 3, 4, 5, 5, 7, 7, 10
また、以下のような場合は、最頻値は存在しないということになります。
1, 3, 4, 5, 7, 10
ヒストグラムの分布と平均値・中央値・最頻値の関係
ヒストグラムの分布で、山のピークが1つの場合、以下が成り立つ場合が多いです。
これを、ピアソンの経験則といいます。
以下の3つのうち、左右対称の場合は必ず成り立ちますが、残りの2つは、経験則なので、必ず成り立つとは限りません。
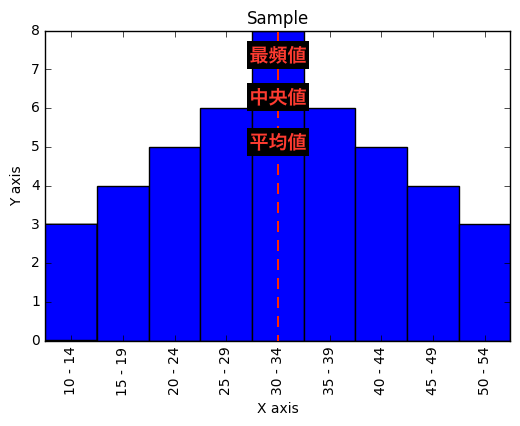
分布が左右対称の場合
ヒストグラムの分布が、以下のように左右対称の場合は、平均値・中央値・最頻値は全て赤い線の位置で、同じとなります。
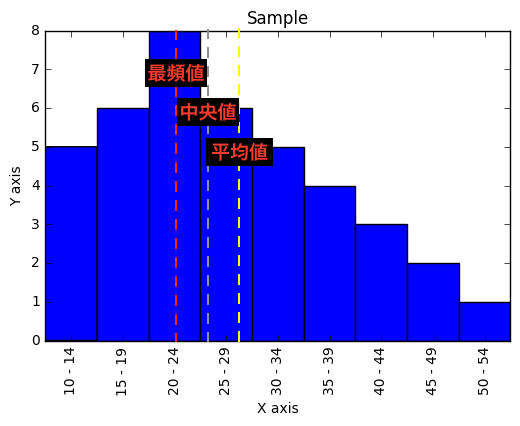
分布が左に偏っている場合
分布が左右対称ではなく左に偏っている(右に裾を引いている)場合、
以下のように、最頻値・中央値・平均値の順で並ぶことが多くなります。
(線は大体の位置に引いています)
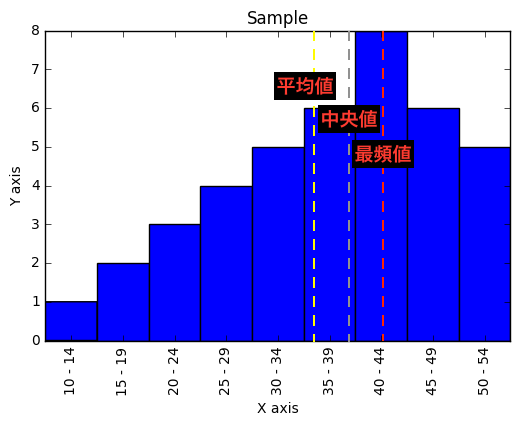
分布が右に偏っている場合
分布が左右対称ではなく右に偏っている(左に裾を引いている)場合、
以下のように、平均値・中央値・最頻値の順で並ぶことが多くなります。
(線は大体の位置に引いています)
どれを代表値とするべきか
平均値・中央値・最頻値のどれを代表値とするべきかは、データの分布によって異なります。
それぞれのメリット、デメリットをまとめました。
| 代表値 | メリット | デメリット |
|---|---|---|
| 平均値 | 全てのデータを反映できる | 極端な値があった場合に引きづられてしまう |
| 中央値 | 極端な値の影響を受けにくい | 真ん中の値以外の変化に気付きにくい |
| 最頻値 | 極端な値の影響を受けにくい | データ数が少ない場合は参考になりにくい |
どれを代表値とするべきかは、データの分布の仕方によって変わります。
基本的には、平均値と中央値の差が少なければ、平均値を代表値とするのがよいかと思います。もし、この2つの差が大きい場合は、中央値と最頻値も見るというやり方が無難なのではと思います。
前述の例のヒストグラムでは、全て山が1つでしたが、山が複数ある場合もあります。
そのような場合、代表値を決めるのは大変ですが、そもそもデータの取り方自体を工夫する必要があるかもしれません。
以上