目次
概要
虚数、複素数を理解するには、実数の理解も必要なので、数全般について説明します。
自然数
指折りで数えることのできる数。0は含まない(含むと定義する場合もある)。
参考:【中学数学】自然数に整数0が含まれないたった1つの理由
厳密な説明に関しては以下を参考
Swiftで自然数を作ってみた(ペアノの公理)
整数
0と負の値を定義し、自然数を拡張した数。
負の値pは以下で定義
p = 0 - n (nは自然数)
つまり、0より小さい値。また、0より大きい値を正の値と呼ぶ。
有理数/無理数
有理数とは分数で表せる数のこと
無理数とは分数で表せない数のこと
有理数
-1.3=-(13/10)
3=3/1=9/3
√0.04=0.2=2/10=1/5
無理数
√3=1.7320508・・・・・
π=3.1415・・・・
実数
実数とは有理数、無理数をまとめた数
とくに実数で直線を表すことができる。
ここまでの数の関係
- 実数
- 有理数
- 整数
- 自然数(正の整数)
- 0
- 負の整数
- 分数
- 整数
- 無理数
- 有理数
虚数
2乗したら0未満になる数を実数に付与した数
とくに実数が0である場合の虚数を純虚数と呼ぶ
例)2i,-1+√3i,1+2i (うち、2iが純虚数)
iは2乗すると-1になる数を表しており、例えば、2iなら以下のように2乗すると-4になる。
※iは虚数の英訳であるimaginary numberの頭文字から
2i \times 2i=(2 \times 2) \times (i \times i)=4 \times (-1)=-4
複素数
複素数とは虚数、実数をまとめた数
例)-1/3, 0, √3i, 3-2i
Q.なぜ虚数(複素数)を定義したか?
A.方程式の解が常に求まるようになるから
例えば)
\begin{align}
(x - 3)^2 &= - 4\\
x &= 3\pm2i
\end{align}
上記に対し、実数までの定義だと解なしが答えとなるが、複素数まで定義すると解を求めることができる。
ちなみに負の整数も自然数の引き算(x=1-5 等)を常に求めることができるようにするために定義した数といえる。
当時は負の数も虚数も架空の数で役に立たないものと考えられていた。
※虚数の英訳であるimaginary number(想像上の数)はその名残
しかし、負の数はいわずもがな、虚数も後に複素数平面等の有用な理論が広まっていき、否定的な意見は完全になくなり受け入れられていくようになった。
参考:
虚数-wikipedia
複素数#歴史-wikipedia
代数学の基本的理-wikipedia
複素数の応用
実数は直線を表していますが、複素数は平面を表しています。
つまり、複素数により平面の各点を表現することができます。
とくに複素数で表現した平面のことを**複素数平面(またはガウス平面)**と呼びます。
やや強引ですが複素数を使うことで、以下のように東だけで各移動が表現できます。
しかも計算が可能!!!(後述参照)
| 原文 | 「東」のみを使って表現 | 式 |
|---|---|---|
| 東に4メートル、北に3メートル進む | 東に4メートル、東に3iメートル進む | 4+3i |
| 東に4メートル、南に3メートル進む | 東に4メートル、東に-3iメートル進む | 4-3i |
| 西に4メートル、南に3メートル進む | 東に-4メートル、東に-3iメートル進む | (-4)+(-3i) |
| 西に4メートル、北に3メートル進む | 東に-4メートル、東に3iメートル進む | -4+3i |
ちなみに実数は直線のため、東と西の2方向しか表現できません
※北西とか南とか表現不可
| 原文 | 「東」のみを使って表現 | 式 |
|---|---|---|
| 東に4メートル進む | 東に4メートル進む | +4 |
| 西に4メートル進む | 東に-4メートル進む | -4 |
掛けるとどうなる?
実数の場合は掛けると拡大・縮小しますが複素数はどうなるのか?
結論から述べれば、拡大・縮小にくわえ、回転します。
簡単な例として、以下の移動にiを掛けた場合を考えてみます。
| 原文 | 「東」のみを使って表現 | 式 |
|---|---|---|
| 東に4メートル、北に3メートル進む | 東に4メートル、東に3iメートル進む | 4+3i |
では、4+3iにiを掛けてみます。
(4+3i) \times i = (4 \times i)+(3i \times i) = 4i-3
4i-3とは、東西南北でいうと、どの状態でしょうか?
北に4メートル、西に3メートルの状態です。
これは、元の座標を、反時計回りに90度回転させた状態です。
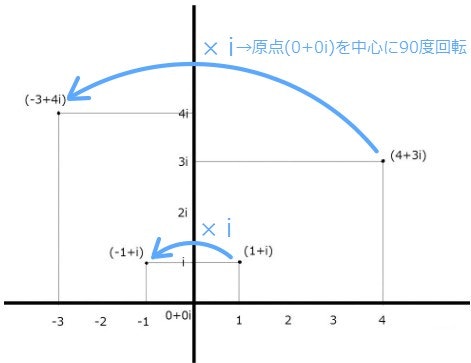
引用元:http://atarimae.biz/archives/500
つまり、iをかけるということは、反時計回りに90度回転させることを意味し、
東に3iメートル進む
というのは、
東から反時計周りに90度回転させた方向(北)に向かって3メートル進む
と同等になります。
ちなみにiを4回掛けると、360度回転するため、元の状態に戻ることになります。
実際に計算すると以下の様に1となります。
i \times i \times i \times i=(-1) \times (-1) = 1
なんとなく、わかりましたか?
ちなみに加減は単純に移動を加減します。
東に4メートル、南に3メートル進み、西に3メートル、南に3メートル進む。
なら、
(4-3i)+(-3-3i) = 1-6i
で東に 1-6iメートル (東に1メートル、南に6メートル)進む
まとめ
- 複素数は方程式の解を常に取得できるようにするための数
- 複素数で平面を表現することができる
おまけ
4次元空間を表現できる数というのもある
四元数-wikipedia
以上
[参考]
虚数とは何か?複素数とは何か?が一気に分かりやすくなる記事
[関連記事]
プログラマーのための数学 - 目次