Go to Qiita Advent Calendar 2024 Top
LoginSignup
170
176

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@EnsekiTT

DeepLearningだ！と意気込んだものの手書き数字認識の後に続かなくなった時に読むデータそのものの話

Last updated at Posted at 2016-03-30

DeepLearningだ！人工知能だ！機械学習だ！

エンジニアとしての意気込みと、
なんだかすごいことが出来そうだな！という上司の後押しを一身に受け、
深層学習本やQiita記事を流し読み、
TensorFlowやChainerを導入して、
チュートリアルの写経で徳を積んで、
ゲームに使っていたGPUも学習という大義名分のもとフル稼働させた、、、

Accuracy 99.23%

今回は、MNISTやIRISを99%超で識別するエンジンを実装して満足してしまったエンジニアが
MNISTを脱却するためにMNISTを知るための話

おなじみ、「MNIST」がつまりどんなデータなのか？

28行28列の画像→正しいが今はそこではない。
データセットとしては、70000行784列、
70000はサンプル数、784は28*28をベクトルに直した時の次元数。
行に解析したいデータ総数、列に解析したいデータ1つ1つだと思っておけば次のステップ(RNNとか？)までは問題ないし、SupportVectorMachineやK-meansも同様の考え方で利用できる。

更にMNISTを観察すると…

手書きの数字はランダムに並んでいるように見える。

これも実は大事で、実務で教師データを集めるときに1を大量に用意して、2を大量に用意して…とやりがち。ちゃんとごちゃごちゃに混ぜてから学習にかける必要がある。
試しに0-8までの数字だけ学習して9を識別できるか試してみて欲しい。きっと0や4が大量に出てくるはずだ。

数字以外がない。

なんて理想的。実務でデータを集めようとすると何かのトラブルで数字のデータセットなのに「A」とか、「-」とかが入っていることもある。
事前に正しく選別されてラベルを付けてもらうことが出来たデータは極めて貴重なのだ。

クラウドファンディングなどでラベルを付けてもらうこともできるので必要に応じて活用しよう。
Captchaを応用した文字集めなども一時期話題になっていた。
ルイス・フォン・アーン ｢ネットを使った大規模共同作業｣
https://www.youtube.com/watch?v=-Ht4qiDRZE8

70000というデータ量

200MB前後。現代のPCのメモリに展開するなら、なんともちょうどいい。
FirefoxでQiitaを見ながら実装して、いきなり実行しても現実的なメモリ使用量で挙動が確認できる。
しかも驚愕するのに十分すぎるほどの識別性能を普通の3層パーセプトロンでも実現できる。

白黒255階層

自然言語処理界隈のように巨大でスパースな行列でもなければ、音声のように長さがバラバラで俯瞰できなわけでもなく、カラフルで3色をうまく扱う必要も特にない。
結果を複数並べてもパット見で判断できる素晴らしさ。中間層で出てくる特徴量もどんなのが優れているか見ればなんとなくわかる。

出したいデータはどんなデータなのか？

MNISTを一通り褒め称えたところで、MNISTで何を出したいか？を考える。
今度は出力のデータの形と教師データにつくラベルの形を理解することを目的とする。

MNISTの例では

1,2,3,4,5,6,7,8,9,0

のどれかを出す。
どんな表現で出て来ると嬉しいか？
例1. 1次元で出力:
6 => 5.5以上6.4以下
7 => 6.5以上7.4以下

例2. 10次元で出力:
6 => [0,0,0,0,0,1,0,0,0,0]
7 => [0,0,0,0,0,0,1,0,0,0]
8 => [0,0,0,0,0,0,0,1,0,0]
多クラス分類であるMNISTでは例2のチュートリアルが多いしそれが適切。
ここで選択を間違えると誤差関数も見当違いのものを選択してしまうことがある。
よしなにやってくれる誤差関数もあるが、一般的でない場合は教師データのラベルに手を入れてあげなきゃいけないことも・・・
この辺の出力に関して明確にしておかないと、2クラス分類や回帰等と混乱してつらい目にあったりする。

結局データを扱うときに気にしてること

  • 次元（固定？可変長？）
  • 値域
  • 単位(対数かどうかや周波数軸かどうかなど
  • 前処理（正規化されてたとしたら何をどう正規化したのかなど)
  • 量
  • 並び
  • 入力方法
  • 確認方法
  • 出力方法
  • 種類(外れ値含むかどうか)
  • 性質(確率分布,離散連続…etc)
  • 他にもあったらコメントください！！！

MNISTに当てはめると

  • 次元：固定784
  • 値域：0-255(物によっては0-1に直されてる)
  • 単位：明るさ(線形)
  • 前処理：特に無し
  • 量：70000（Train 60000, Test 10000）
  • 並び：ランダム
  • 入力方法：全てのデータセットを一気に入力可能、後から増えたりしない
  • 確認方法：28*28の画像として確認可能
  • 出力方法：0-9の数字
  • 種類(外れ値含むかどうか)：0-9の数字のみ
  • 性質(確率分布,離散連続…etc)：数字の出現確率は一様

実際に気にしていることを確認してみる。

WhatMnist.py
import pandas as pd
import numpy as np
# Chainer
import chainer
import chainer.functions as F
import chainer.links as L
from chainer import optimizers
from chainer import serializers, Variable
# 可視化(Jupyter想定)
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm

PKLの場合

WhatMnist.py
# http://deeplearning.net/data/mnist/mnist.pkl.gz
# タプルで(train, valid, test)
# train -> (data, label)
# valid -> (data, label) 親切すぎてValidationデータまで分かれてる
# test -> (data, label)
# Pandasを使ってデータを読み込む
mnist = pd.read_pickle('mnist.pkl')

http://deeplearning.net/tutorial/gettingstarted.html
データセットはこちら。

CSVの場合

WhatMnist.py
if(0):
    # Pandas + csvの場合
    mnist = pd.read_csv('mnist.csv') 
    # Numpy + csvの場合
    mnist = np.loadtxt('mnist.csv')
    # ラベル列の分離(最初の行がラベルと仮定)
    mnist_data, mnist_label = np.split(mnist, [1], axis=1)
    # 学習行とテスト行のsplit
    x_train,x_test = np.split(mnist_data, [50000])
    y_train,y_test = np.split(mnist_label, [50000])

データ形式の確認

WhatMnist.py
print('## 次元と量')
print("train.data:{0}, train.label:{1}".format(mnist[0][0].shape, mnist[0][1].shape))
print("valid.data:{0}, valid.label:{1}".format(mnist[1][0].shape, mnist[1][1].shape))
print("test.data:{0}, test.label:{1}".format(mnist[2][0].shape, mnist[2][1].shape))

print('## 値域と単位')
print("train.data.max:{0}, train.data.min:{1}".format(np.max(mnist[0][0]), np.min(mnist[0][0])))
print("train.label.max:{0}, train.label.min:{1}".format(np.max(mnist[0][1]), np.min(mnist[0][1])))

print('## 並びと出力方法')
print("head -n 30 label: {0}".format(mnist[0][1][:30]))

print('## 入力方法(一気に読み込んでnp.arrayに突っ込んである)')
fig = plt.figure()
ax1 = fig.add_subplot(2,1,1)
ax2 = fig.add_subplot(2,1,2)
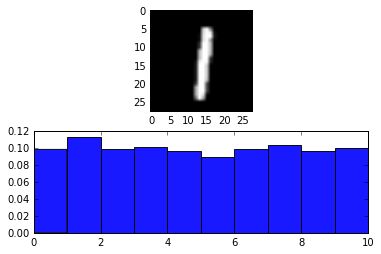
print('## 確認方法')
print('代表として適当なものを表示してみた。')
ax1.imshow(mnist[0][0][40].reshape((28,28)), cmap = cm.Greys_r)

print('## 種類と性質')
print('ここではヒストグラムで各クラスの頻度を可視化してみた。')
ax2.hist(mnist[0][1], bins=range(11), alpha=0.9, color='b', normed=True)

次元と量

train.data:(50000, 784), train.label:(50000,)
valid.data:(10000, 784), valid.label:(10000,)
test.data:(10000, 784), test.label:(10000,)

値域と単位

train.data.max:0.99609375, train.data.min:0.0
train.label.max:9, train.label.min:0

並びと出力方法

head -n 30 label: [5 0 4 1 9 2 1 3 1 4 3 5 3 6 1 7 2 8 6 9 4 0 9 1 1 2 4 3 2 7]

入力方法(一気に読み込んでnp.arrayに突っ込んである)

確認方法

代表として適当なものを表示してみた。

種類と性質

ここではヒストグラムで各クラスの頻度を可視化してみた。
(array([ 0.09864, 0.11356, 0.09936, 0.10202, 0.09718, 0.09012, 0.09902, 0.1035 , 0.09684, 0.09976]),
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]),
mnisthist.png

今後のために呼び出しやすい名前をつける

chainerではデータをfloat32,int32で扱い、arrayとして扱う(CPUでは)

WhatMnist.py
x_train = np.array(mnist[0][0], dtype=np.float32)
y_train = np.array(mnist[0][1], dtype=np.int32)
x_test = np.array(mnist[2][0], dtype=np.float32)
y_test = np.array(mnist[2][1], dtype=np.int32)
print('x_train:' + str(x_train.shape))
print('y_train:' + str(y_train.shape))
print('x_test:' + str(x_test.shape))
print('y_test:' + str(y_test.shape))

x_train:(50000, 784)
y_train:(50000,)
x_test:(10000, 784)
y_test:(10000,)

後はお馴染みチュートリアル

WhatMnist.py
# 予測器クラス
class MLP(chainer.Chain):
    def __init__(self):
        super(MLP, self).__init__(
            l1=L.Linear(784, 100),
            l2=L.Linear(100, 100),
            l3=L.Linear(100, 10),
        )
    
    def __call__(self, x):
        h1 = F.relu(self.l1(x))
        h2 = F.relu(self.l2(h1))
        y = self.l3(h2)
        return y
    
# LossとAccuracyを計算する
class Classifier(chainer.Chain):
    def __init__(self, predictor):
        super(Classifier, self).__init__(predictor=predictor)
        
    def __call__(self, x, t):
        y = self.predictor(x)
        self.loss = F.softmax_cross_entropy(y, t)
        self.accuracy = F.accuracy(y, t)
        return self.loss

model = Classifier(MLP())
optimizer = optimizers.SGD()
optimizer.setup(model)

batchsize = 100
datasize = 50000
for epoch in range(20):
    print('epoch %d' % epoch)
    indexes = np.random.permutation(datasize)
    for i in range(0, datasize, batchsize):
        x = Variable(x_train[indexes[i : i + batchsize]])
        t = Variable(y_train[indexes[i : i + batchsize]])
        optimizer.update(model, x, t)

学習結果を使う

(個人的にはこっちの工夫が大事だと思ってる。)

WhatMnist.py
n = 10
x = Variable(x_test[n:n+1])
v = model.predictor(x)
plt.imshow(x_test[n:n+1].reshape((28,28)), cmap = cm.Greys_r)
print(np.argmax(v.data))

0
show.png

おわりに

DeepLearningの波が来るはるか昔の話。
機械学習を細々とやっていた時に、雑魚院生だった私はアルゴリズムやコーディングに目が行きがちでデータそのものの性質を見失うことが多かった。
量が多くなるほど観察しにくいものを観察しないといけなくなるし、性質への理解が性能に大きく効いてくる。道に迷ったらデータを見よう。

さあ、チュートリアルのその先へ

170
176
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
170
176

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?