やりたいこと
以下のように表される、平均$\mu$、分散$\sigma^2$のガウス分布を考えます。
\mathcal{N}(x\,\lvert\,\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{1}{2\sigma^2}(x-\mu)^2\right)
あるN個のデータ、$x_1,x_2\cdots x_N$を観測したとします。
それぞれのデータが上記のガウス分布に従って独立に生成されたとした時に、データからガウス分布の平均$\mu$、分散$\sigma^2$の値を推定します。
そして、その推定値が、真の値と比べてどうであるかを評価します。
平均と分散の推定
期待値を${\mathbb E}[\cdot]$で表します。
つまり、
\mathbb{E}[x] = \mu\\
\mathbb{E}[x^2] = \mu^2 + \sigma^2\\
\mathbb{E}[(x-\mu)^2] = \sigma^2
また、観測データをまとめて、
{\bf x} = (x_1,x_2\cdots x_N)^T
と表します。
ガウス分布からN個のデータを生成した時に、それらが観測データ${\bf x}$と一致する確率は、各データ$x_1\sim x_n$それぞれが生成される確率の掛け算になるので、
p({\bf x}\,\lvert\,\mu,\sigma^2) = \prod_{n=1}^N\mathcal{N}(x_n\,\lvert\,\mu,\sigma^2)
となります。これを、「尤度」と呼びます。
この確率「尤度」を最大にする、$\mu,\sigma^2$を求めたいのですが、$\exp$や、$\prod$が入っており計算しにくいです。
そこで、両辺の対数をとり、以下のように計算しやすくします。
\ln p({\bf x}\,\lvert\,\mu,\sigma^2) = \sum_{n=1}^N(x_n -\mu)^2 - \frac{N}{2}\ln{\sigma^2} - \frac{N}{2}\ln{2\pi}
$y = \ln(x)$は、以下のように$x$が増えるとyも増加する関数です。
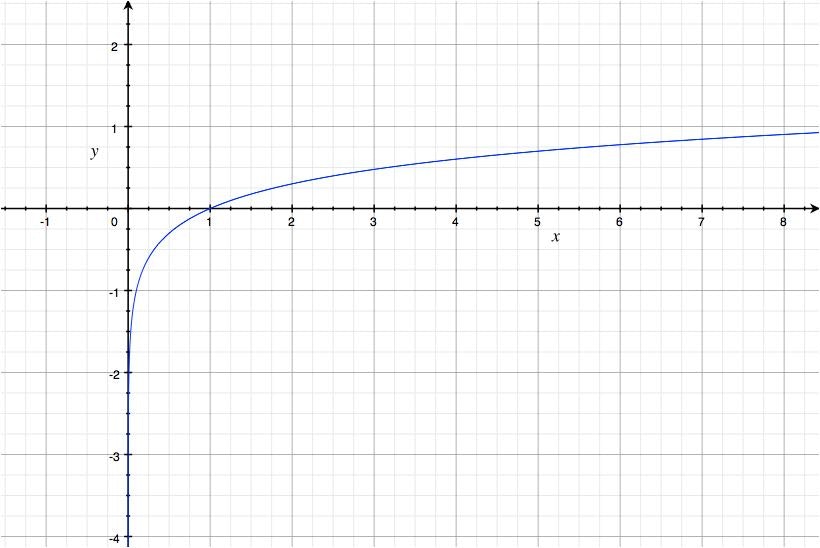
なので、$p({\bf x},\lvert,\mu,\sigma^2)$の最大化と、$\ln p({\bf x},\lvert,\mu,\sigma^2)$の最大化は同じ意味を持ちます。
$\mu,\sigma^2$について微分して0とおくことで、以下のようになります。
\mu_{ML} = \frac{1}{N}\sum_{n}x_n\\
\sigma^2_{ML} = \frac{1}{N}\sum_{n}(x_n - \mu_{ML})^2
なお、求めた値を、真の値と区別する意味で、$\mu_{ML},\sigma^2_{ML}$としています。
真の値との比較
平均と分散の真の値を、$\mu,\sigma^2$とします。
様々なデータ${\bf x}を使って、$$\mu_{ML},\sigma^2_{ML}$の推定を行った時に、$\mu_{ML},\sigma^2_{ML}$はどのような値をとる可能性が高いかを調べてみます。具体的には、$\mu_{ML},\sigma^2_{ML}$の期待値を考えます。
平均に関しては、
\begin{align}
\mathbb{E}[\mu_{ML}] &= \frac{1}{N}\sum_{n}\mathbb{E}[x_n]\\
&=\mu
\end{align}
となり、真の平均に一致します。
一方分散に関しては、
\begin{align}
\mathbb{E}[\sigma^2_{ML}] &= \frac{1}{N}\sum_{n}\mathbb{E}[(x_n - \mu_{ML})^2]\\
&=\frac{1}{N}\sum_{n}\left(\mathbb{E}[x_n^2] - 2\mathbb{E}[x_n\mu_{ML}] + \mathbb{E}[\mu_{ML}^2]\right)
\end{align}
ここで、$\mu_{ML}$は、データ点を元に計算される値であることに注意すると、
\begin{align}
\frac{1}{N}\sum_{n}\mathbb{E}[x_n\mu_{ML}] &= \frac{1}{N}\sum_{n}\mathbb{E}[x_n\frac{1}{N}\sum_{m}x_m]\\
&=\frac{1}{N^2}\sum_{n}\sum_{m}\mathbb{E}[x_nx_m]\\
&=\frac{1}{N}\left(\sigma^2 + N\mu^2\right)
\end{align}
\begin{align}
\frac{1}{N}\sum_{n}\mathbb{E}[\mu_{ML}^2] &= \frac{1}{N}\sum_{n}\mathbb{E}[\frac{1}{N}\sum_{l}x_l\frac{1}{N}\sum_{m}x_m]\\
&=\frac{1}{N^3}\sum_{n}\sum_{l}\sum_{m}\mathbb{E}[x_lx_m]\\
&=\frac{1}{N}\left(\sigma^2 + N\mu^2\right)
\end{align}
となるので、
\mathbb{E}[\sigma^2_{ML}] = \frac{N-1}{N}\sigma^2
となり、分散の推定値は、真の値よりも小さな値をとる可能性が高いことが分かります。この現象を、バイアスと呼ぶそうです。
実装1
# !/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
# プロット用データ
X=np.arange(1,5,0.001)
def gaussian(x,mu,sig2):
y=np.exp(((x-mu)**2)/(-2*sig2))/np.sqrt(2*np.pi*sig2)
return y
# 真の平均・分散
mu=3
sig2=1.0
# 一回の最尤推定に利用するデータ数
N=2
# 最尤推定を行う回数
M=10000
# N個を一セットとして、Mセットのデータを真の分布から生成
x=np.sqrt(sig2)*np.random.randn(N,M)+mu
# N個のデータを利用した最尤推定を、Mセット分実施
mu_ml=(1/N)*x.sum(0)
sig2_ml=(1/N)*((x-mu_ml)**2).sum(0)
# 真の分布
plt.plot(X,gaussian(X,mu,sig2),'r',lw=15,alpha=0.5)
# M回の最尤推定の結果を平均した分布
plt.plot(X,gaussian(X,mu_ml.sum(0)/M,sig2_ml.sum(0)/M),'g')
# 最尤推定値の分散をN/N-1倍して、バイアスを取り除いたもの
plt.plot(X,gaussian(X,mu_ml.sum(0)/M,sig2_ml.sum(0)/M * N/(N-1)),'b')
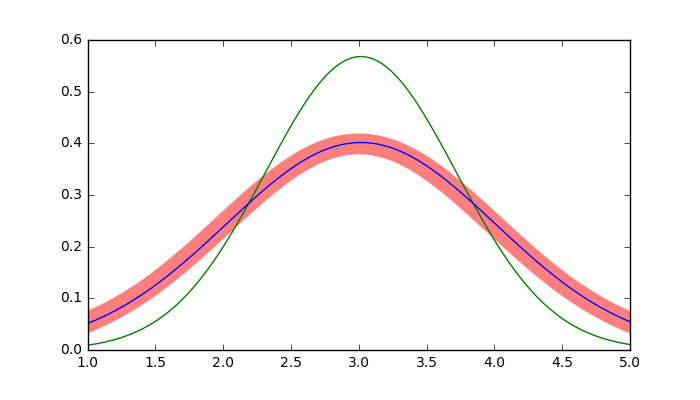
実行結果1
最尤推定値(緑線)の分散を、$\frac{N}{N-1}$倍したもの(青線)と、真の分布(赤太線)が一致していることがわかります。
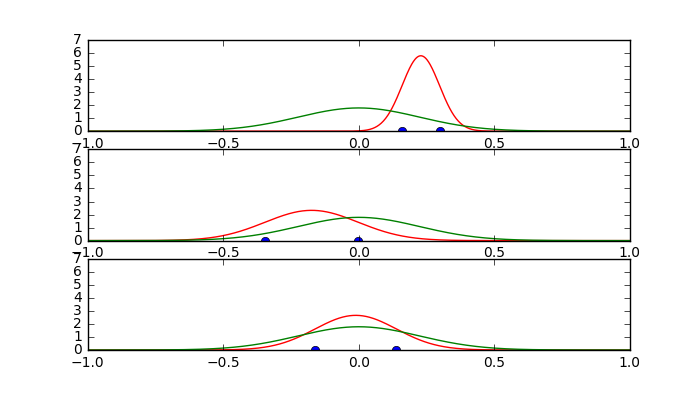
実装2
# !/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
# プロット用データ
plotS = 1000
X = np.linspace(-1,1,plotS)
# ガウス分布の確率密度関数
def gaussDist(x,mu,sig2):
ret = np.exp(-(x-mu)**2/(2*sig2))/np.sqrt(2*np.pi*sig2)
return ret
# 真の分布
mu_r = 0
sig2_r = 0.05
Y_r = gaussDist(X,mu_r,sig2_r)
np.random.seed(10)
for i in range(3):
plt.subplot(3,1,i+1)
plt.ylim([0,7])
#訓練データ
N = 2
x_t = np.random.randn(N) * np.sqrt(sig2_r) + mu_r
plt.plot(x_t,np.zeros(x_t.shape[0]),'bo')
#最尤推定した分布
mu_ML = x_t.sum()/N
sig2_ML = ((x_t - mu_ML)**2).sum()/N
Y_ml = gaussDist(X,mu_ML,sig2_ML)
plt.plot(X,Y_ml,'r')
#真の分布
plt.plot(X,Y_r,'g')