PRMLの図作成 図1.4 多項式曲線フィッティング

多項式曲線フィッティングとは

回帰における、一番基礎となるアルゴリズムです。
のちに出てくるベイズ線形回帰や、ニューラルネットワーク、ガウス過程などのアルゴリズムは、確率論が加えられたり、あるいは、より高次元空間に適用できるように工夫されたりしていますが、基本的な部分は共通しています。

やりたいこと

ある入力 $\boldsymbol{x} = (x_1,x_2,\cdots,x_N)^T$および、出力 $\boldsymbol{t} = (t_1,t_2,\cdots,t_N)^T$　を観測したとします。(Nはデータの個数)
このとき、新たな入力$x$に対する出力$t$を予測したいとします。
これを、「回帰問題」といいます。

ここで、ある関数$y(x)$を考えます。この関数に、$x_1,x_2,\cdots,x_N$をそれぞれ代入したときに、出力$y(x_1),y(x_2),\cdots,y(x_N)$が、 $t_1,t_2,\cdots,t_N$に近い値になったとすれば、新たな入力$x$に対する出力$t$は、$y(x)$と一致する可能性が高いと考えられます。

多項式曲線フィッティングでは、パラメータ$\boldsymbol{w} = (w_0,w_1,\cdots,w_M)^T$を導入し、以下の多項式を考えます。(Mは多項式の次元：固定パラメータとする。)

y(x, \boldsymbol{w})=w_0+w_1x^1+w_2x^2+{\cdots}w_Mx^M= \boldsymbol{w}^T\boldsymbol{\phi}(x)

ただし、$\boldsymbol{\phi}(x) = (1,x,x^2,\cdots,x^M)^T$

また、この関数に$x_1,x_2,\cdots,x_N$を代入した結果を、次のようにまとめておきます。

\boldsymbol{y}(\boldsymbol{x}, \boldsymbol{w})=(y(x_1, \boldsymbol{w}),y(x_2, \boldsymbol{w}),\cdots,y(x_N, \boldsymbol{w}))^T=\boldsymbol{\Phi}\boldsymbol{w}

ただし、$\boldsymbol{\Phi} = (\boldsymbol{\phi}(x_1),\boldsymbol{\phi}(x_2),\cdots,\boldsymbol{\phi}(x_N))^T$

この$\boldsymbol{y}(\boldsymbol{x}, \boldsymbol{w})$と、$\boldsymbol{t}$をできる限り一致させる、$\boldsymbol{w}$を求めます。そのために、まず両者の差分をとって、2乗します。

\begin{align}
E(\boldsymbol{w}) &= (\boldsymbol{y}(\boldsymbol{x}, \boldsymbol{w})-\boldsymbol{t})^T(\boldsymbol{y}(\boldsymbol{x}, \boldsymbol{w})-\boldsymbol{t})\\
&=\boldsymbol{w}^T\boldsymbol{\Phi}^T\boldsymbol{\Phi}\boldsymbol{w} - 2\boldsymbol{t}^T\boldsymbol{\Phi}\boldsymbol{w} +\boldsymbol{t}^T\boldsymbol{t}
\end{align}

この誤差$E(\boldsymbol{w})$をできるだけ小さくする$\boldsymbol{w}$を求めたいので、$\boldsymbol{w}$で微分して$0$とおくと、

\begin{align}
\frac{dE(\boldsymbol{w})}{d{\boldsymbol{w}}} &=2\boldsymbol{\Phi} ^T\boldsymbol{\Phi}\boldsymbol{w} - 2\boldsymbol{\Phi}^T\boldsymbol{t} = 0
\end{align}

これを解いて、

\boldsymbol{w} =(\boldsymbol{\Phi} ^T\boldsymbol{\Phi})^{-1}\boldsymbol{\Phi}^T\boldsymbol{t}

となります。
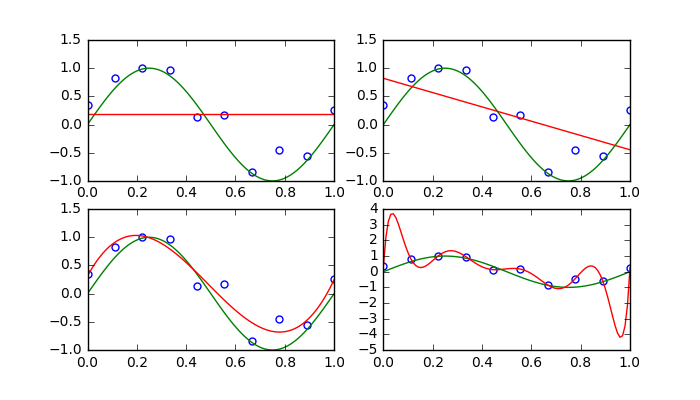
では、実装してみます。

ソースコード

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


import numpy as np
import matplotlib.pyplot as plt


#訓練データ
data = np.array(
        [[0.000000,0.349486],
         [0.111111, 0.830839],
         [0.222222, 1.007332],
         [0.333333, 0.971507],
         [0.444444, 0.133066],
         [0.555556, 0.166823],
         [0.666667, -0.848307],
         [0.777778, -0.445686],
         [0.888889, -0.563567],
         [1.000000, 0.261502]])

x=data[:,0]
t=data[:,1]


#プロット用データ
plotS = 100
X = np.linspace(0,1,plotS)
Y = np.zeros(plotS)


def _phi(xn,M):
    ret = np.zeros([M+1])
    for m in range(M+1):
        ret[m] += xn**m
    return ret


def _Phi(x,M):
    N = x.shape[0]
    ret = np.zeros([N,M+1])
    for n in range(N):
        ret[n,:] = _phi(x[n],M)
    return ret


plotArea = 0
for M in [0,1,3,9]:
    #wの学習
    Phi = _Phi(x,M)
    w = np.linalg.inv(Phi.T.dot(Phi)).dot(Phi.T).dot(t)

    plotArea += 1
    plt.subplot(2,2,plotArea)

    #訓練データのプロット
    plt.plot(x,t,'o',c='w',ms=5,markeredgecolor='blue',markeredgewidth=1)

    #真の曲線のプロット
    plt.plot(X,np.sin(2 * np.pi * X),'g')

    #近似曲線のプロット
    for i in range(plotS):
        Y[i] = w.dot(_phi(X[i],M))
    plt.plot(X,Y,'r')

実行結果