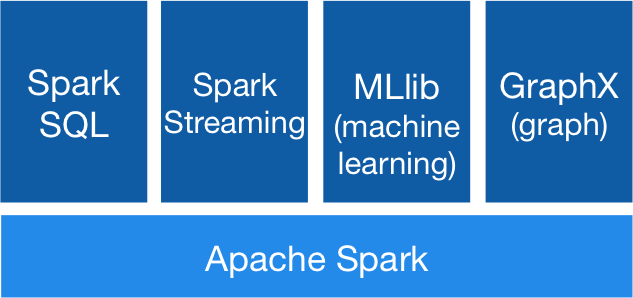
Spark GraphXとは?
Spark GraphXとはSparkという分散計算処理基盤の上に構築された4兄弟の一人です。
ネットワークグラフ(ネットワークデータベース)を主に扱います。
ネットワークグラフとは具体的にはTwitterのフォロー・フォロワーのつながりのネットワークなどが該当します。
エンタメ系だとアニメやドラマ作品でよくある人物相関図が該当するでしょう。
ライブラリは貧弱ですが、数個だけアルゴリズムが実装されておりその中の一つにページランクアルゴリズムがあります。
- Spark https://spark.apache.org/
- Spark GraphX https://spark.apache.org/graphx/
- グラフ理論
ページランクアルゴリズムとは
Googleのページ検索で使われているアルゴリズムで、多くリンクされているページが信頼度が高いという指標にもとづいてページがスコアリングされるアルゴリズムになります。
Spark GraphX ページランクアルゴリズム検証
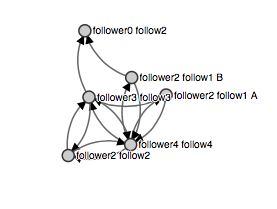
Spark GraphXのページランクアルゴリズムの実装が正しいものなのか、意図した通りの結果がでるか検証するため、Twitterのフォロー・フォロワーの関係をサンプルデータとして投入します。
マスターデータ(ユーザーIDに紐づく名前を入れておくファイル)
1,follower4 follow4
2,follower3 follow3
3,follower2 follow2
4,follower2 follow1 A
5,follower2 follow1 B
6,follower2 follow0
コネクションデータ(フォロー・フォロワーの関係をユーザーID
1 2
1 3
1 4
1 5
2 1
2 3
2 6
3 1
3 2
4 1
4 2
5 1
5 6
D3.jsで図にしたもの
Graph Node JS Viewで簡単にグラフ図に変換できます。
ScalaでSpark GraphXページランクアルゴリズムを使う
コードは公式サイトのサンプルをちょと改良しただけで以下のようなコードになります
import org.apache.spark.graphx.{Graph, GraphLoader}
import org.apache.spark.{SparkConf, SparkContext}
/**
* Created by AKB428 on 2015/06/03.
*/
object TwitterFollowerScoreRanking2 {
def main(args: Array[String]): Unit = {
// https://spark.apache.org/docs/latest/quick-start.html
val conf = new SparkConf().setAppName("TwitterFollowerScoreRanking2")
conf.setMaster("local")
val sc = new SparkContext(conf)
// 元データを読み込み
val graph: Graph[Int, Int]
= GraphLoader.edgeListFile(sc, args(0)).cache()
// https://spark.apache.org/docs/latest/graphx-programming-guide.html#pagerank
// Run PageRank
val ranks = graph.pageRank(0.0001).vertices
// Join the ranks with the usernames
val users = sc.textFile(args(1)).map { line =>
val fields = line.split(",")
(fields(0).toLong, fields(1))
}
val ranksByUsername = users.join(ranks).map {
case (id, (username, rank)) => (username, rank)
}
// Print the result
println(ranksByUsername.collect().mkString("\n"))
sc.stop()
}
}
実行結果
SBTのコンソールで以下のように実行します。
run connection.txt master.txt
(follower4 follow4,0.8537194616353887)
(follower3 follow3,0.696904254070486)
(follower2 follow2,0.5288329792246881)
(follower2 follow0,0.4882131211233435)
(follower2 follow1 A,0.3313979135584405)
(follower2 follow1 B,0.3313979135584405)
結果から以下のことがわかります。
- フォロワー、フォローが双方とも一番大きい人がスコアが一番高い
- 同じフォロワー数2でも、フォロー数によってスコアが異なる follow2 > follow0 > follow1
ツイッターやってる人なら納得いく結果ではないでしょうか?
ちゃんと計算できているようなので他の問題もSpark GraphX で計算してみましょう。
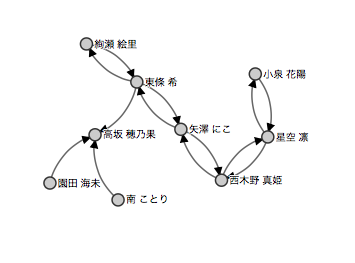
Spark GraphX で「ラブライブ!」の登場人物のカップリングを計算してみる
マスターデータ(キャラクターデータ)
1,高坂 穂乃果
2,南 ことり
3,園田 海未
4,西木野 真姫
5,星空 凛
6,小泉 花陽
7,矢澤 にこ
8,絢瀬 絵里
9,東條 希
以下のデータはだいたいあってると思いますが独断と偏見で算出しました。
コネクションデータ(恋愛の矢印的な・・)
2 1
3 1
4 5
4 7
5 4
5 6
6 5
7 4
7 9
8 9
9 8
9 7
9 1
D3.jsで表した図
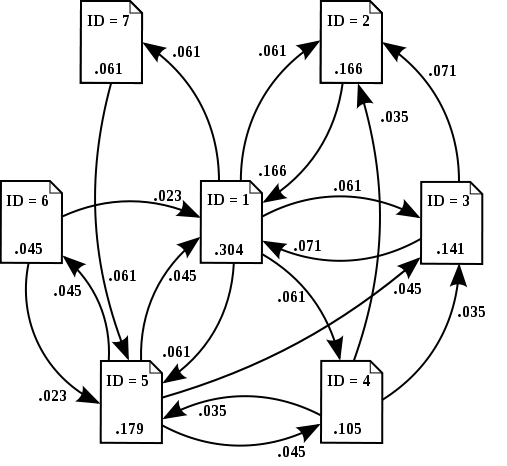
実行結果
run ../GraphNodeView_D3js/lovelive/coupling.txt ../GraphNodeView_D3js/lovelive/character.txt
(星空 凛,1.0463409909749495)
(西木野 真姫,0.9201159065091673)
(東條 希,0.7938914688181047)
(矢澤 にこ,0.765854808354306)
(高坂 穂乃果,0.629871865514959)
(小泉 花陽,0.5946949211643535)
(絢瀬 絵里,0.37487186551495905)
(南 ことり,0.15)
(園田 海未,0.15)
なんと星空凛ちゃんが一番スコアが高くなりました。
二人とコネクションでつながっているメンバーは星空凛にもいます(矢澤にこ、東條希、西木真姫)が左のフォローワーがいないキャラクター(南ことり、園田海未)と繋がってることで左側の人達のスコアが低くなってるようです。
かなり正確にとページランクアルゴリズムが実装されているのがわかります。
単純なスコアリングなら独自で実装できると思いますがここまでの計算は独自で実装するのは大変そうです。
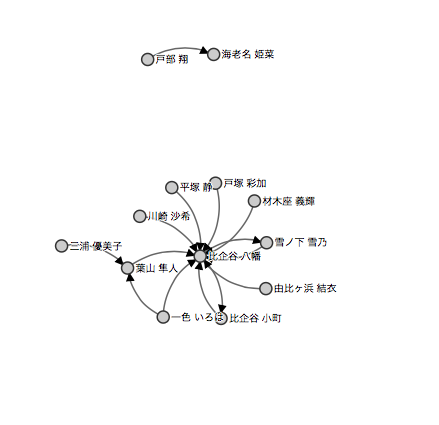
Spark GraphX で「やはり俺の青春ラブコメはまちがっている。」の登場人物のカップリングを計算してみる
ハーレムラノベと言われると刺されそうですがハーレムラノベのキャラクター相関図も解析してみましょう。
マスターデータ
1,比企谷 八幡
2,雪ノ下 雪乃
3,由比ヶ浜 結衣
4,平塚 静
5,戸塚 彩加
6,材木座 義輝
7,川崎 沙希
8,葉山 隼人
9,三浦 優美子
10,海老名 姫菜
11,戸部 翔
12,一色 いろは
13,比企谷 小町
コネクションデータ (恋愛の矢印的なもの)
1 2
1 13
2 1
3 1
4 1
5 1
6 1
7 1
8 1
9 8
11 10
12 8
12 1
13 1
D3.js 図
実行結果
run ../GraphNodeView_D3js/oregairu/coupling.txt ../GraphNodeView_D3js/oregairu/character.txt
(比企谷 八幡,5.0306006042500275)
(比企谷 小町,2.2880052568062625)
(雪ノ下 雪乃,2.2880052568062625)
(葉山 隼人,0.34124999999999994)
(海老名 姫菜,0.27749999999999997)
(一色 いろは,0.15)
(戸塚 彩加,0.15)
(平塚 静,0.15)
(戸部 翔,0.15)
(材木座 義輝,0.15)
(由比ヶ浜 結衣,0.15)
(川崎 沙希,0.15)
(三浦 優美子,0.15)
コネクションデータが正しいならそこまで間違ってる結果ではないと思います。
かなり面白いです。
現実的な問題に適用するためじゃんけんをSprak GraphXで計算してみる
まったくノード数はないですが、GraphXは現実的な問題も対処できるんだぜ!アピールするためにじゃんけんも解析してみます。
実際にはじゃんけんを国家(軍事力)や政党やスポーツチームに変えてみましょう。
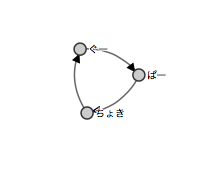
ノーマルじゃんけん
マスターデータ
1,ぐー
2,ちょき
3,ぱー
コネクションデータ 負ける相手をフォローしてると考える
1 3
2 1
3 2
D3.js 図
実行結果
run ../GraphNodeView_D3js/PaperScissorsSociety/win-lose.txt ../GraphNodeView_D3js/PaperScissorsSociety/master.txt
(ぐー,0.9994334078112798)
(ぱー,0.9994334078112798)
(ちょき,0.9994334078112798)
当たり前ですが同列スコアになりました。
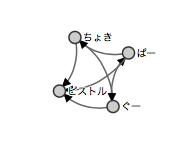
ピストル込のじゃんけん
マスターデータ
1,ぐー
2,ちょき
3,ぱー
4,ピストル
コネクションデータ
1 3
2 1
3 2
1 4
2 4
3 4
D3.js 図
実行結果!
run ../GraphNodeView_D3js/PaperScissorsSocietyAndPistool/win-lose.txt ../GraphNodeView_D3js/PaperScissorsSocietyAndPistool/master.txt
(ピストル,0.4824582311787476)
(ぐー,0.26081941039291584)
(ぱー,0.26081941039291584)
(ちょき,0.26081941039291584)
当たり前ですがピストルさん強いです。
ですがぶっちぎりというわけではなくページランクではスコは ピストル:その他 で 48 : 26 ということがわかります。