これは言語実装 Advent Calendar 2016の4日目の記事です。
こちらは一般的なプログラミング言語の処理系とは目的も作り方も全く異なる言語処理系について、勉強して実際に作ってみようという企画となります。
今回は動作記述からハードウェア記述言語へとコンパイルする高位合成コンパイラがテーマです。元々はこの１回で単純なコンパイラの実装までを完結させるつもりでしたが、実装が間に合いませんでしたので、カレンダーの空いている日をもう１日頂いて１日目を勉強編、２日目を実装編という事にしたいと思います。
今回は、知人に紹介を頂きました以下の論文を勉強する事にしました。結構typoや組版崩れが多いので読む際は注意してください。回路設計の分野は非常に広範なのでもちろんこの論文の手法が全てではありません。
Chaiyakul, Viraphol, and Daniel D. Gajski. Assignment decision diagram for high-level synthesis. Information and Computer Science, University of California, Irvine, 1992.
以下、記載に誤りがございましたら是非ご指摘頂けますと幸いです。
高位合成とは
論理回路はレジスタ転送レベル(RTL)という抽象表現で記述する事が出来ます。具体的な言語としてはVerilogやVHDL等が用いられます。
論理回路は大別して①組合せ回路と②順序回路からなります。組合せ回路はAND,OR,NOT等のゲートの組合せからなり入力から一意的に出力が定まります。一方、順序回路は状態を持つ回路でレジスタを用いて構成されます。
(引用 https://en.wikipedia.org/wiki/Register-transfer_level)
RTLでの回路記述は大雑把に言うと
- 回路内で使用されるレジスタを宣言し
- レジスタとレジスタを繋ぐ組合せ回路を記述する
という形式になります。以下はVHDLでの回路の記述例(フィボナッチ数列の計算)です。
(引用: https://ja.wikipedia.org/wiki/VHDL 、注記を追加)
-- Fib.vhd
--
-- Fibonacci number sequence generator
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.numeric_std.all;
-- 注記: I/Oポートの宣言
entity Fibonacci is
port
(
Reset : in std_logic;
Clock : in std_logic;
Number : out unsigned(31 downto 0)
);
end entity Fibonacci;
architecture Rcingham of Fibonacci is
-- レジスタ・ワイヤの宣言(どっちになるかは回路合成ツールのコンパイラが決定)
signal Previous : natural;
signal Current : natural;
signal Next_Fib : natural;
begin
Adder:
Next_Fib <= Current + Previous; -- 加算を行う組合せ回路
Registers:
process (Clock, Reset) is
begin
if Reset = '1' then -- リセット信号が立った時
Previous <= 1;
Current <= 1;
elsif Clock'event and Clock = '1' then -- クロック毎にレジスタをアップデート
Previous <= Current;
Current <= Next_Fib;
end if;
end process Registers;
Number <= to_unsigned(Previous, 32);
end architecture Rcingham;
このようにRTLでの記述は、通常の手続き的なプログラミング言語とは大分様子が異なります。(例えばNext_Fib <= Current + Previousの部分はハードウェア的に常時加算を行っているわけで、「AしてBしてCして」という手続き的な考え方に慣れていると戸惑う所かと思います。)
さて、高位合成とはC言語やJava等の通常のプログラミング言語による動作の記述から、VerilogやVHDL等のRTLでの記述へと変換する事によって回路設計を行う方法の事を言います。
Assignment Decision Diagram
高位合成行う際に、動作記述を直接RTL表現に変換するのは大変なので一旦中間表現に変換します。
今回読んだ上記の論文ではAssignment Decision Diagram (ADD)という表現を提案しています。この表現が他の表現に比べてどうかという話は分からないので適当な事書けませんから割愛します。論文によれば
One of the ultimate goal in the research on representation for synthesis is the search of a unique representation.
という事です。unique representationというのはセマンティック的に同じプログラムは同じ表現に変換されるという事です。既存の表現ではセマンティック的に同一でも記述方法が少し異なるだけで全く異なる表現に変換されてしまうという問題があるらしいです。
ADDとは
ADDは5つの要素から構成されます。
- Assignment Values
- Assignment conditions
- Assignment decision
- Assignment target
- Assignment index
そして各要素は4種のノードで構成されます。
- Operation Nodes
- Read Nodes
- Write Nodes
- Assignment Decision Nodes (ADNs)
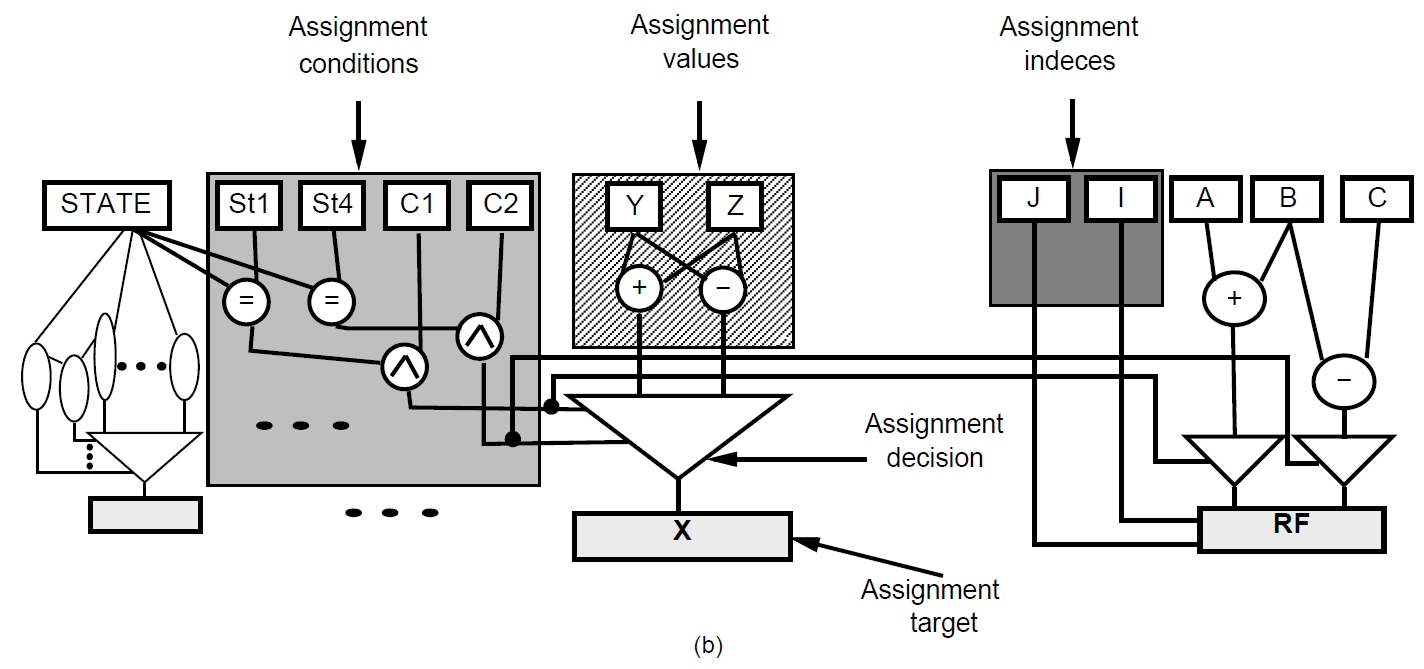
(引用: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.9420&rep=rep1&type=pdf のFigure 1-b)
Read Nodeはレジスタ、メモリ、Inputポート、定数を表します。Write Nodeはレジスタ、メモリ、Ouptutポートを表します。
Assignment ValueパートはRead Nodeの値を用いてWrite Nodeに書き込まれるべき値を計算する回路を表現します。
Assignment Conditionパートは同じくRead Nodeの値の値を用いてブール値を計算する回路です。Write Nodeへの代入に対する条件付けを行う回路です。
Assignment DecisionパートはADNで構成され、Assignment Valueパートが計算した値とAssignment Conditionパートが計算した値にもとづいて、Write Nodeに書き込むべき値の選択を行います。
Assignment TargetパートはWrite Nodeからなり、ADNが選択した値がここに出力されます。上の図だとSTATE == St1 && C1のときにX <= Y+Z、STATE == St4 && C2のときにX <- Y-Zとなるような状況を表しています。
Assignment IndexパートはRead NodeもしくはWrite Nodeが配列の場合に使用されます。上の図だとSTATE == St1 && C1のときにRF[I] <= A + B、STATE == St4 && C2のときにRF[J] <= B-Cとなるような状況が表されています。RF[I]、RF[J]への代入は並列にできるのでADNは別々にあります。(I == Jのときはどうなるのかというのは後述)
Assignment Value, Assignment Conditionパートの計算部は(命令列ではなく)データフローグラフで表現します。ADD全体は無向グラフとして表現されます。
ADDのText表現
グラフ形式で議論するのは大変なので、テキスト表現を導入します。
$$ \alpha = \langle \beta_0\{\gamma_0\}\oplus \beta_1\{\gamma_1\}\oplus\cdots \oplus \beta_m\{\gamma_m\}\rangle[\theta_0],\langle \cdots \rangle[\theta_1],\ldots,\langle\cdots\rangle[\theta_n]. $$
(論文では$\beta_n\{\gamma_n\}$となっていますが恐らく誤りなので修正)
$\alpha$はAssignment Targetか、ワイヤー上のシグナルを表します。$\beta$はAssignment condition、$\gamma$はAssignment value, $\theta$はassignment indexを表現します。例えば先程の図の一部は
\begin{align}
temp1_{(type:signal)} &= \{STATE=St1\wedge C1\}. \\
temp2_{(type:signal)} &= \{STATE=St4\wedge C2\}. \\
X_{(type:storage)} &= temp1\{Y + Z\}\oplus temp2\{Y-Z\}. \\
RF_{(type:storage)} &= \langle temp1\{A+B\}\rangle [I], \langle temp2\{B-C\}\rangle [J].
\end{align}
というように表されます。
VHDLとADDの対応
続いてADDとRTL表現の例であるVHDLの対応について重要そうな所を説明します。
型
Write Node, Read Nodeの型は３つの情報で表現されます。
- type: signal, port or storage
- dim: スカラ変数なら1, 配列なら2
- size: ビット幅
例えば16bit × 8のstorageタイプの配列変数は
$$ A_{(type:storage,dim:2,sz:(16,8))} $$
と表されます。
代入
VHDLには2種類の代入文
A <= B + C;
A := B + C;
が存在します。前者は具体的なポートやワイヤへの出力を表していて、実際のハードウェアと対応するものです。後者はプログラムを記述する為に一時的に用いられる変数への代入で、実際のハードウェアと対応するものではありません。
ADDでは先程の型を用いてこれらを区別します。type = port, signalの場合は<=、storageの場合は:=に相当するものと考えます。
条件文
例えば
case (C + E) is
when "0001" => A <= "0100";
when "0101" => A <= "1111";
...
end case;
は
\begin{align}
temp0_{(type:signal,dim:1,size:4)} &= \{C + E\}.\\
temp1_{(type:signal,dim:1,size:1)} &= \{temp0 = \rm{"0001"} \}. \\
temp2_{(type:signal,dim:1,size:1)} &= \{temp0 = \rm{"0101"} \}. \\
&\vdots \\
A_{(type:signal,dim:1,size:4)} &= temp1\{\rm{"0100"}\}\oplus temp2\{\rm{"1111"}\}\oplus\cdots .
\end{align}
と対応します。ifやwhenも同様なので省略します。
ループ
ループを表現するのは若干面倒です。状態を表現する事が必要になるので特別なレジスタ$State\_register$を導入します。
例えば
D := 0;
while (D < E) loop
A := D + A;
D := D + 1;
end loop;
は(A,D,Eが4ビットとすると)
\begin{align}
temp_{(type:signal,dim:1,size:1)} &= \{D < E\}. \\
State\_register &= ST_2\{ST_0\}\oplus ((ST_0\wedge temp)\vee (ST_1\wedge temp))\{ST_1\}\oplus ((ST_0\wedge \overline{temp})\vee (ST_1\wedge \overline{temp}))\{ST_2\}.\\
A_{(type:storage,dim:1,size:4)} &= ST_1\{D+A\}. \\
D_{(type:storage,dim:1,size:4)} &= ST_0\{{\rm "0000"}\}\oplus ST_1\{D+{\rm "0001"}\}.
\end{align}
となります。$ST_x$ は
$$ State\_register = STx $$
という条件の略です。
$ST_0$はループに入る前、$ST_1$はループ内部、$ST_2$はループを抜けた後を表します。
$ST_2\{ST_0\}$は論文中にそう記載があるのでここにも書いていますが、これは必須ではないような。
固定長のfor文の場合はunrollできる場合にはそのようにすれば良いです。
ADDを用いた高位合成
ADDへの変換
まず入力プログラムをADDへ変換します。この方法については
や
に記載があります。簡単に説明すると、ステートメント単位でADDへの変換を行いつつ、それをマージしていくという手順になります。
(引用元: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.8694&rep=rep1&type=pdf のFigure 8)
各ステートメントの変換は単純なので割愛しますがマージは面倒です。というのは同じ変数が複数のステートメントで参照される場合のData Dependencyの問題を解決しなければならない為です。
上の図は(元のプログラムにおいて)ADD1の後にADD2が実行される状況でのマージを表していますが、ADD1でXに代入した後、ADD2でそれを読むread after write (RAW) dependency、ADD1でRFに代入した後、ADD2でもRFに代入するwrite after write (WAW) dependency, Cを読んだあとまた読む read after read (RAR) dependencyが存在します。
回路設計では可能な限り並列に動作させたいので、ADD1の完了を待ってからADD2を実行するというようにはしたくありません。そこでRAW dependencyの場合は上の図の様に、ADD1の計算結果と条件を複製してADD2のX - BのXを置き換えています。またRFは配列ですのでI != Jの場合は並列に代入出来ますが、I == Jの場合はADD2の方の代入を行うというようなADDが生成されています。
他にもwrite after read (WAR) dependencyやread after read (RAR) dependencyに関しても同様の変換が行われます。詳細は割愛します。
静的単一代入形式(SSA形式)に予め変換しておくとこのあたりは大分効率良くなると予想出来ます。実際にそのような手法が使われているようです。
SchedulingとBinding
ADDへの変換が終わったら、計算のスケジューリングと演算器やインターコネクトの割当(binding)が必要になります。このスケジューリングは手続き型言語のそれとは大分雰囲気が異なります。
そもそも何のために操作かというと、タイミングの制約とリソースの制約を解決する為のものです。つまりADDのRead NodeからWrite Nodeまでのパスが1 clock以内に計算出来ないかもしれないという問題や、演算器やレジスタ等のリソースが足りないかもという問題を解決しなければいけません。
下図はALU 1つ(加算や比較)と乗算器1つしかないハードウェアの場合の例です。図の様にstate boundaryを挿入する事によってスケジューリングを行い、タイミングやリソースの問題を解決していきます。図中のMergeとあるのは、同時に実行される事がない演算に対して一つの演算器を割り当てる操作です。
(引用元 http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.9420&rep=rep1&type=pdf のFigure 17)
上の図は直感的な理解の為の図で、実際には下図の様にADDに変換を加える事によってこの操作を実現します。従って中間表現としてのADDの構造はそのままです。
(引用元 http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.9420&rep=rep1&type=pdf のFigure 21-b)
このschedulingとbindingの問題を一気に問いてしまう事は困難で、反復的にこの手順を行います。つまりstate boundaryを挿入して、resourceを割り当て、次のstate boundaryを挿入して、…という感じです。
タイミングやリソース使用量の推定
SchedulingやBindingを行う為には、ADDの状態でタイミングや使用されるリソースについて推定する事が必要になります。これらについてはまた別の論文を読まなければいけません。例えば、
いきなりこのあたりをギリギリまで攻めるのは荷が重いと思いましたので、とりあえずは動作させる事を目指して単純な実装でやることにしようと思います。
Scheduling, Bindingまでが終われば上の方で書いたVHDLとADDの対応関係に基いて変換をするのみとなります。
まとめ
動作記述からRTL表現へ変換する方法についてその流れを勉強しました。またその中間表現としてAssignment Decision Diagram (ADD) 表現の紹介を行いましたが、よくあるコンパイラとは大分異なる表現を必要とする事が分かりました。ADDの理論の中でも最適化の関わる以下の部分は非常に難しく奥が深そうです。
- ADDへの変換(特にADDのマージ)において、如何に回路の並列性を損なわないようにするか。
- Scheduling, Bindingを如何に上手くやるか。
次回は実際にコンパイラを作って回路を動作させる所を目指します。