Markov Logic Network(MLN) というモデルについて勉強した際のノートです。誤りがあるかもしれませんのでご注意下さい。とりあえず使う為にはAlchemyのようなソフトウェアもあります。Matthew RichardsonとPedro Domingosの論文を読みたいと思います。
Markov Logic Network
概要
Markov Logic Network $L$ とは
一階述語論理の論理式 $F_i$ と実数値の重み $w_i$ の組 $(F_i, w_i)$ の集合
の事。例えば下のようなもの。
$\forall x(\rm{Smokes}(x)\Rightarrow \rm{Cancer}(x)): 1.5$
$\forall x\forall y(\rm{Friends}(x,y)\Rightarrow (\rm{Smokes}(x)\Leftrightarrow\rm{Smokes}(y))): 2.2$
$\rm{Smokes}(x),\rm{Cancer}(x),\rm{Friends}(x,y)$などの単一の述語と幾つかの項からなる記号列を原子論理式(atomic formula)と言い、これから結合記号や量化記号を用いて一般の論理式が構成される。変数を含まない論理式 $\rm{Smokes}(Anna)$ などをground formula(日本語でなんという?)と言う。
実用上、論理式を**連言標準形(Conjunctive Normal Form, CNF)にして考える。各選言は節(clausal form)**と呼ばれる。上の論理式の組は以下の3つの節の連言として書ける。
$F_1: \neg\rm{Smokes}(x)\vee\rm{Cancer}(x): 1.5$
$F_2: \neg\rm{Friends}(x,y)\vee \neg\rm{Smokes}(x)\vee\rm{Smokes}(y): 1.1$
$F_3: \neg\rm{Friends}(x,y)\vee \rm{Smokes}(x)\vee\neg\rm{Smokes}(y): 1.1$
ただし、一つの論理式が複数のclauseからなる場合はもともとの重みを等配分する。
Markov Logic NetworkはProbabilistic Logicのモデルの一つで、通常のLogicと違うのは論理的な言明が絶対成り立つのではなくて「ほぼ必ず成り立つ」とか「多分成り立つ」とか「もしかしたら成り立つ」などの曖昧性を持つという所。重み $w_i$ がこの度合いと関係していて、$w_i$が大きいほどより成り立つ可能性が高いという事になる。上の例では、「友人同士はお互い喫煙者か非喫煙者である」という法則の方が「喫煙者は癌になる」という法則よりも少しだけ確からしいという事を表している。
Markov Network
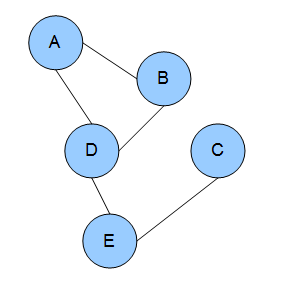
以下、各確率変数が有限個の値を取りうる離散確率変数の場合を考える。Markov Networkというのは確率変数間の条件付き独立性を無向グラフを用いて表現したモデル。各頂点に確率変数が紐付いているが、面倒だから頂点と確率変数を同一視して説明する。変数の集合 $S$が固定された時に、これによって分断された変数の集合$X,Y$が互いに独立になる。例えば以下のグラフ(wikipediaより)では「変数$D$の値が所与ならば、$A$と$E$は独立になる」などの条件付き独立性が表現される。
ここで乗法定理より
$P(A,B,C,D,E) = P(A,B|C,D,E)P(C,D,E) = P(A,B|C,D,E)P(D|C,E)P(C,E)$
と分解できるが、グラフで表現された条件付き独立性を使うと
$P(A,B,C,D,E) = P(A,B|D)P(D|E)P(C,E)$
となる。つまり適当な関数$\phi_1,\phi_2,\phi_3$があって
$P(A,B,C,D,E) \propto \phi_1(A,B,D)\phi_2(D,E)\phi_3(C,E)$
と書ける。この$\{A,B,D\},\{D,E\},\{C,E\}$はクリーク(完全な部分グラフ)になっている。
このような表現は一般に出来て、Markov Networkで表現された確率モデルは、グラフ$G$の各クリーク$C$毎に定義されたクリークポテンシャル(clique potential) $\phi_C$を用いて
$$ P(X=x) = \frac{1}{Z}\prod_{C}\phi_C(x_C) $$
と書くことが出来る。これを**クリーク因子分解(clique factorization)という。$Z$はいわゆる正規化定数だけれども、統計力学に由来する用語で分配関数(partition function)**とも呼ばれる。
このモデルは**対数線形モデル(Log-linear model)**の形に書くことも出来る。まず$x_C$の取りうる値が$n_C$通り$a_{C,1},\ldots,a_{C,n_C}$の時
$$ P(X=x) = \frac{1}{Z}\prod_{C}\prod_{k=1}^{n_C}\phi_C(a_{C,k})^{f_{C,k}(x)}\qquad \left(\mbox{$f_{C,k}(x)$は$x_C=a_{C,k}$ならば1それ以外ならば$0$}\right)$$
と書ける。$\phi_C(a_{C,k})$は正の定数だからこれを$w_{C,k} = \log \phi_C(a_{C,k})$とおくと
$$ P(X=x) = \frac{1}{Z}\prod_{C}\prod_{k=1}^{n_C}\exp\left(w_{C,k}f_{C,k}(x)\right) = \frac{1}{Z} \exp\left(\sum_C\sum_{k=1}^{n_C}w_{C,k}f_{C,k}(x)\right)$$
と書けて、添字$\{C,k\}$を連番で振り直せば
$$ P(X=x) = \frac{1}{Z}\exp\left(\sum_i w_if_i(x)\right) $$
という形になる。$f_i$を**素性関数(feature function)**とか特徴関数と言って、今見たように$\{1,0\}$を取る様にする事が多い。
Markov Logic Network
Markov Logic Network $L$と有限の定数集合 $C$から、Markov Network $M_{L,C}$が定義される。
$M_{L,C}$のグラフ構造は以下のように定義される。
- 頂点: $L$内の各atomの各groundingが2値の確率変数である。
- 辺: $L$の同一のground formulaに含まれるground atom間に辺を引く。
上の $L$ と$C=\{A,B\}$ の場合、$L$内のatom、$\rm{Smokes}(x),\rm{Cancer}(x),\rm{Friends}(x,y)$の可能なgroundingは
$\rm{Smokes}(A), \rm{Smokes}(B), \rm{Cancer}(A), \rm{Cancer}(B), \rm{Friends}(A, A),\rm{Friends}(B, B),\rm{Friends}(A, B),\rm{Friends}(B, A)$
なので8頂点のグラフとなり、ground formula
$\rm{Smokes}(A)\Rightarrow \rm{Cancer}(A)$
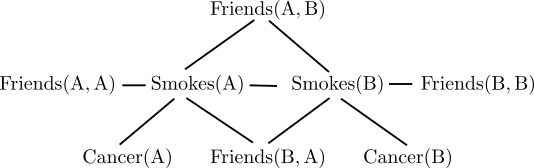
に対応して$\rm{Smokes}(A)$と$\rm{Cancer}(A)$間に辺を引く。他のground formulaについても同様。絵に書くと以下のようになる。
このグラフで表現されている条件付き独立性について考えてみる。例えば$\rm{Cancer}(A)$と$\rm{Smokes}(B)$はパスが繋がっているので従属。$A$がガンを患っているか否かの情報が、$A$が喫煙者か否かに関する確信度に影響し、$A,B$は友達の可能性があるからこれは$B$が喫煙者か否かに関する確率にも影響を及ぼす。一方、$\rm{Smokes}(A)$が既知の場合には、$\rm{Cancer}(A)$から$\rm{Smokes}(B)$へのパスが無くなるのでこれらは独立となる。$A$がガンを患っているか否かの情報を得ても、$A$が喫煙者か否かは既知でその確率は$0$もしくは$1$から変わりようが無いから、$B$が喫煙者か否かの確率にも影響を及ぼさないという事だと解釈できる。
$M_{L,C}$の確率分布は論理式$F_i$の各ground formulaについてそれが真となるなら$1$、偽なら$0$をfeatureとし、featureの重みを$w_i$として定まるLog-linear model。同じ論理式は常に同じ重みだから結局
$$P(X=x|M_{L,C}) = \frac{1}{Z}\exp\left(\sum_i w_in_i(x) \right)\quad (\mbox{$n_i(x)$は$x$によって$F_i$が真となった回数})$$
というシンプルな形に整理される。
計算例
例えば$x$が
$\rm{Smokes}(A)=True, \rm{Smokes}(B)=True$
$\rm{Friends}(A,A)=\rm{Friends}(B,B)=False, \rm{Friends}(A,B)=\rm{Friends}(B,A)=True$
$\rm{Cancer}(A)=True, \rm{Cancer}(B)=False$
の場合を考えると、$F_1$に関して
$\neg\rm{Smokes}(A)\vee\rm{Cancer}(A)$
のみが成立してるので$n_1(x)=1$
$F_2$に関して
$\neg\rm{Friends}(A,A)\vee\neg\rm{Smokes}(A)\vee\rm{Smokes}(A)$
$\neg\rm{Friends}(B,B)\vee\neg\rm{Smokes}(B)\vee\rm{Smokes}(B)$
$\neg\rm{Friends}(A,B)\vee\neg\rm{Smokes}(A)\vee\rm{Smokes}(B)$
$\neg\rm{Friends}(B,A)\vee\neg\rm{Smokes}(B)\vee\rm{Smokes}(A)$
の全てが成立するので$n_2(x)=4$、同様にして$n_3(x)=4$。したがって
$$P(X=x|M_{L,C}) = \frac{1}{Z}\exp\left(1.5\times 1 + 1.1\times 4+1.1\times 4\right) = \frac{1}{Z}e^{10.3}$$
となる。このような計算をあらゆる$X=x$($2^8=256$通り)に対して行って、確率の和が$1$となるように$Z$を求める。大変だから計算機でやると以下のようになる。アルゴリズム的な工夫はあとでやる。
import pandas as pd
import numpy as np
from scipy.misc import logsumexp
from itertools import product
const = ['A', 'B']
preds = [('Smokes', 1), ('Cancer', 1), ('Friends', 2)] # Predicate and arity
ground_atoms = [
(p, *args)
for p, arity in preds
for args in product(const, repeat=arity)
]
print('=== Ground Atoms ===')
print(ground_atoms)
formulas = [
# (atom, negation, arity, weight)
([('Smokes', (0,)), ('Cancer', (0,))], [1, 0], 1, 1.5),
([('Friends', (0,1)), ('Smokes', (0,)), ('Smokes', (1,))], [1, 0, 1], 2, 1.1),
([('Friends', (0,1)), ('Smokes', (0,)), ('Smokes', (1,))], [1, 1, 0], 2, 1.1)
]
ground_formulas = []
for clauses, neg, arity, w in formulas:
for args in product(const, repeat=arity):
ground_formula = [
(p, *map(lambda i: args[i], v))
for p, v in clauses
]
ground_formulas.append((ground_formula, neg, w))
print('=== Ground Formulas ===')
print(ground_formulas)
# Generate all configurations
X = pd.DataFrame(columns=ground_atoms, data=list(product([1, 0], repeat=len(ground_atoms))))
# Compute sum_i(w_i*n_i(x))
S = np.zeros(len(X))
for f, neg, w in ground_formulas:
S += w * np.logical_xor(X[f], neg).any(1)
# Compute partition function
logZ = logsumexp(S)
# Compute joint probabilities
jointP = X.copy()
jointP['logP'] = S - logZ
print('=== Joint Probability ===')
print(jointP)
あとは適当に変数をsumming outしたりして任意の確率分布を計算出来る。pandasのgrouping機能を使うと直感的に書けて良い。
# Examples
print('=== P(Friends(A, B)) ===')
P_FrAB = np.exp(jointP.groupby([('Friends', 'A', 'B')])['logP'].agg(logsumexp))
print(P_FrAB)
print('=== P(Friends(A, B)|Smokes(A)) ===')
P_FrAB_SmoA = np.exp(jointP.groupby([('Smokes', 'A'), ('Friends', 'A', 'B')])['logP'].agg(logsumexp))
P_SmoA = np.exp(jointP.groupby([('Smokes', 'A')])['logP'].agg(logsumexp))
print(P_FrAB_SmoA/P_SmoA)
結果は以下。
=== P(Friends(A, B)) ===
(Friends, A, B)
0 0.570909
1 0.429091
Name: logP, dtype: float64
=== P(Friends(A, B)|Smokes(A)) ===
(Smokes, A) (Friends, A, B)
0 0 0.553456
1 0.446544
1 0 0.605285
1 0.394715
Name: logP, dtype: float64
この世界では$A,B$が友達である確率は42.9%、但し$A$が喫煙者の場合この確率は39.5%となるといった事が分かった。
置かれている仮定
後回しにしていたけれども、Markov Logic Networkの構成において以下の3つの仮説が置かれている。
- Unique names: 異なる定数記号は異なる対象を表す。
- Domain closure: $(L, C)$内の定数と関数を用いて構成される対象しか存在しない。
- Known functions: $L$内の任意の関数を任意の対象に適用した結果は既知であり、それは$C$に含まれる。
それぞれの仮定は緩める事が出来る。例えば仮定1を置く代わりに$\rm{Equals}(x,y)$という述語を導入するなど。詳しくは論文にある。
存在量化子の取り扱い
存在量化子が含まれる論理式例えば
$\forall x\exists y\rm{Friends}(x,y)$
の取り扱いだけれども、Domain closure仮定より$y$の動く範囲は既知で有限だからそられの選言として展開してしまえば良い。例えば $C=\{A,B\}$である世界では
$\forall x\exists y\rm{Friends}(x,y)$
と
$\forall x(\rm{Friends}(x,A)\vee\rm{Friends}(x,B))$
は同値となる。
(続く)