組み合わせの列挙

組み合わせを列挙しようとして手が止まりました。基本的なアルゴリズムのはずなのに、いざ実装しようとすると思いのほか難しいです。検索してみると同じように感じた方が多いようで、色々な実装が出て来ました。屋上屋を架すことにはなりますが、試みた実装を説明します。

【追記 2020.01.05】実装を大幅に変更しました。

方針

手作業で組み合わせを列挙する場合、次のように考えます。

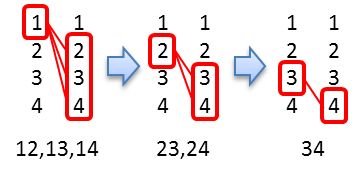
【例】 {1,2,3,4} から2個を取り出した組み合わせ

これをなるべく素直に実装してみようと考えました。

特徴

挙動を観察すると、次のような特徴が分かります。

• 左の数字＜右の数字（組み合わせでは順番を区別しないため、便宜的な取り決め）
• {1,2,3}のそれぞれに、それより大きい数字を組み合わせます。{4}はそれより大きい数字がないため左には来ません。

実装

1つ小さい数字までの組み合わせ combination (n - 1) (k - 1) の末尾に、それより大きい数字を追加します。

let rec combination n = function
| k when k < 1 -> []
| 1 -> [ for i in 1..n -> [i] ]
| k -> [ for c in combination (n - 1) (k - 1) do
         for i in (List.max c) + 1 .. n -> List.append c [i] ]

printfn "%A" (combination 4 2)

実行結果

[[1; 2]; [1; 3]; [1; 4]; [2; 3]; [2; 4]; [3; 4]]

メモ化

n や k が大きくなると構築に時間が掛かるようになります。プログラム中で何度も使う場合、結果をキャッシュしておくと効果的です。これをメモ化と呼びます。

F#

let memoize (f: 'k -> 'v) =
    let cache = System.Collections.Generic.Dictionary<'k, 'v>()
    fun a ->
        let b, v = cache.TryGetValue a
        if b then v else
        let ret = f a
        cache.[a] <- ret
        ret

let   curry f = fun a  b  -> f(a, b)
let uncurry f = fun(a, b) -> f a  b

let combination =
    let rec f n = function
    | k when k < 1 -> []
    | 1 -> [ for i in 1..n -> [i] ]
    | k -> [ for c in g (n - 1) (k - 1) do
             for i in (List.max c) + 1 .. n -> List.append c [i] ]
    and g = f |> uncurry |> memoize |> curry
    g

再帰の結果もキャッシュするため相互再帰しています。