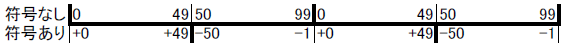符号あり数値をなるべく直感的に説明します。
※ 意図的に「最上位ビットが符号を表す」ことから話を始めませんので、ご了承ください。
暗算の工夫
$12+99$ を暗算で計算するとき、どのように計算するでしょうか。計算の得意な方なら特に工夫しなくてもそのまま計算できるかもしれませんが、そうでない場合には少し工夫すると計算が簡単になります。
$99$ が $100$ の1つ前であることを利用して $12+100-1$ と読み替えます。そうすれば繰上りに煩わされることなく $111$ とすぐに計算できます。
2桁に制限された世界
もし計算結果を2桁に制限するという条件が付いていたら、結果はどうなるでしょうか。
$12+99=12+100-1=111⇒11$
2桁に制限された時点で $100$ が $0$ になって消えていると見なせます。
$12+99=12+100-1 ⇒ 12-1=11$
つまり $+99$ と $-1$ が同一視できる結果となります。
このことから次のことが推測できます。
- 桁数が制限された計算では、大きな数の足し算が実質的に引き算となる。
※ この $0$ ~ $99$ のように制限された数の集合を有限体と呼びます。
補数
$99$ は $100-1$ から求めていますが、同様の関係を任意の数に適用する方法を考えます。
引く数と答えを逆にします。
$100-1=99 ⇒ 100-99=1$
このように $100$ から引くことでお互いを変換できます。
$100-a=b ⇔ 100-b=a$
※ この $a$ と $b$ のような関係を補数と呼びます。
符号の線引き
足し算と引き算の対応関係を見ていきます。
- $x+1 ⇔ x-99$
- $x+2 ⇔ x-98$
- (略)
- $x+49 ⇔ x-51$
- $x+50 ⇔ x-50$
- $x+51 ⇔ x-49$
- (略)
- $x+98 ⇔ x-2$
- $x+99 ⇔ x-1$
第2項のみを取り出して、計算だけでなく数としても対応していると見なします。
- $+1 ⇔ -99$
- $+2 ⇔ -98$
- (略)
- $+49 ⇔ -51$
- $+50 ⇔ -50$
- $+51 ⇔ -49$
- (略)
- $+98 ⇔ -2$
- $+99 ⇔ -1$
中央の $50$ を境に絶対値の大小関係が逆転します。大きな数は符号反転して考えることにより、絶対値が小さい方で解釈するように決めます。
その際に中央値がどちらに属するか決める必要があります。個数を基準に考えれば中央値をマイナスに割り振れば均等となります。つまり絶対値の最大(この場合は $50$)はマイナス側に含まれます。
| 符号なし | 符号あり | 個数 |
|---|---|---|
| 0~49 | +0~+49 | 50 |
| 50~99 | -50~-1 | 50 |
このようにして符号あり数値が得られました。
視覚化
2桁に制限された世界では $+1$ を繰り返すと桁があふれて $0$ に戻ります。つまり数が循環します。このことを数直線で表現すると、符号の有無によって別々の箇所で不連続となる2つの循環する数の重なりが見えて来ます。
※ 循環していることから円による描き方もできます。
符号なしと符号ありに対応関係があり相互に変換できるのがポイントです。
16進数
同じ理屈を16進数に適用すると、いわゆる整数型が作れます。
| サイズ | 符号なし | 符号あり |
|---|---|---|
| 1バイト | 0~0xFF | -0x80~0x7F |
| 2バイト | 0~0xFFFF | -0x8000~0x7FFF |
| 4バイト | 0~0xFFFFFFFF | -0x80000000~0x7FFFFFFF |
符号なしで表現できる数値の上半分が、符号ありでのマイナスとなります。これをビットで見ると、最上位ビットが符号を表すことになります。
参考
符号ビットによる通常の説明はWikipediaを参照してください。