【Unity2D】Unityで2Dゲームをつくるときに知っておきたいコンポーネント・クラスのまとめ

はじめに

Unityで2Dゲームをつくるときに、よく使うコンポーネントやクラスをまとめてみました。

コンポーネント

Unityはコンポーネント指向という設計で作られています。ゲームオブジェクトに、必要な機能をコンポーネントとして追加することで機能拡張できるようになっています。

なおスクリプト上でコンポーネントを取得するには、GetComponent関数を使います。

Rigidbody2Dを取得する

// Rigidbody2Dを取得する
Rigidbody2D rd = GetComponent<Rigidbody2D>();

2D関連のコンポーネントはさまざまなものがありますが、以下のものが比較的よく使われます。
なお、この中で「Transform」のみゲームオブジェクトに必須のコンポーネントとなっており、ゲームオブジェクト作成時にデフォルトで用意されています。

コンポーネント名	概要	リファレンス
Sprite Renderer	スプライト表示	http://docs.unity3d.com/jp/current/ScriptReference/SpriteRenderer.html
Transform	位置・回転・スケール	http://docs.unity3d.com/jp/current/ScriptReference/Transform.html
Rigidbody 2D	物理挙動	http://docs.unity3d.com/jp/current/ScriptReference/Rigidbody2D.html
Collider 2D	2Dの衝突判定	http://docs.unity3d.com/jp/current/ScriptReference/Collider2D.html
BoxCollider2D	2Dの矩形の衝突判定	http://docs.unity3d.com/jp/current/ScriptReference/BoxCollider2D.html
CircleCollider2D	2Dの円の衝突判定	http://docs.unity3d.com/jp/current/ScriptReference/CircleCollider2D.html

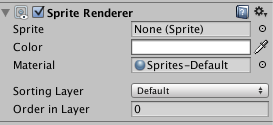
Sprite Renderer

スプライトを表示するコンポーネントです。

よく使うと思われるメンバ変数は以下のものとなります。

型	変数名	概要	Inspector上での名称
bool	enabled	スプライトの表示(true)・非表示(false)を制御するフラグ	チェックボックス
Sprite	sprite	描画対象のスプライト。この変数に直接代入することで、描画するスプライトを切り替えることができる	Sprite
Color	color	描画するスプライトの頂点カラー（色）。例えば、赤色と白色を交互に指定すれば、赤く点滅することができる。なおColorのメンバ変数 r / g / b はそれぞれRGBカラーで、メンバ変数の「a」はアルファ値。取りうる値は 0.0〜1.0	Color
string	sortingLayerName	ソーティングレイヤー名。レイヤー名を指定することで、描画レイヤーを設定できる	Sorting Layer
int	sortingOrder	ソーティングレイヤー内での描画順。数値が大きいほど手前に（上に）描画される	Order in Layer
Bounds	bounds	描画のバウンディングボリューム（領域）。Boundsクラスのメンバ変数のsizeがこの領域の大きさを保持しているので、bounds.size.x でスプライトの幅、bounds.size.y でスプライトの高さを取得できる	-

Transform

オブジェクトの位置、回転、スケールを扱うコンポーネントです。

よく使うと思われるメンバ変数は以下のものとなります。

型	変数名	概要	Inspector上での名称
Vector3	position	ワールド空間における位置情報。この値を変更することで直接ゲームオブジェクトを移動させることができる。ただし通常、ゲームオブジェクトを動かす場合はRigidbody 2Dを使うほうがよい	Position
Vector3	localScale	スケール値。2Dゲームでは x / y 成分のみ変更する	Rotation
Vector3	eulerAngles	回転角度。2Dゲームでは通常 Z軸 の回転のみ行う	Scale

各変数の値の変更について

それぞれの値は、Vector3の成分を直接指定することはできません。

☓間違った例

// ☓間違った例
transform.position.x = 100;

値を変更するには、以下のように一時変数にpositionの値をコピーして、positionに対して代入を行います。

○正しい例

// ○正しい例
// 一時変数に格納
Vector3 pos = transform.position;
// 値を変更
pos.x = 100;
// 代入する
transform.position = pos;

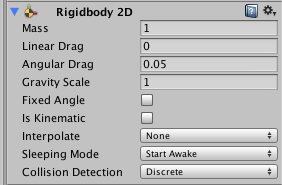
Regidbody 2D

物理挙動を制御するコンポーネントです。

Transform.positionからでも移動することはできるのですが、これを使うとタイムスケールの変更(特に可変フレームレート下での動作)に対して自動で移動速度を調整してくれるという恩恵を受けることができます。また、コリジョンを適切に設定すれば、他のゲームオブジェクトの衝突時に自動で反発する挙動もしてくれます。
よく使うメンバ変数は以下のものです。

型	変数名	概要	Inspector上での名称
Vector2	velocity	移動速度	-
float	angularVelocity	回転速度	-
float	angularDrag	回転に対する抵抗係数	Angular Drag
float	gravityScale	重力	Gravity Scale
bool	fixedAngle	回転を許可するかどうか	Fixed Angle

角度と速度から移動速度を割り出す場合

移動速度のメンバ変数である velocity はVector2(x / y)のため、角度指定で特定の方向へ移動させることができません。
角度指定で移動速度を決定したい場合は以下のように記述します。

角度と速さを指定した移動量の設定

// 40度方向に5の速度で移動する
float direction = 40.0f;
float speed = 5.0f;
Vector2 v;
v.x = Mathf.Cos(Mathf.Deg2Rad * direction) * speed;
v.y = Mathf.Sin(Mathf.Deg2Rad * direction) * speed;

Rigidbody2D rd = GetComponent<Rigidbody2D>();
rd.velocity = v;

また移動方向を取得するには以下のように記述します。

移動方向の取得

// 移動方向を取得する
Rigidbody2D rd = GetComponent<Rigidbody2D>();
Vector2 v = rd.velocity;
return Mathf.Atan2 (v.y, v.x) * Mathf.Rad2Deg;

Collider2D

2Dの衝突を判定するコンポーネントです。Unityはコライダーと呼ばれるコンポーネントをオブジェクトにアタッチすることで、衝突を行うことができます。
ただ、実際に使う場合は派生クラスの BoxCollider2D (矩形コライダー)や CircleCollider2D (円形コライダー)を使うこととなります。
よく使うかもしれないメンバ変数は以下のとおりです。

型	変数名	概要
bool	enabled	衝突判定を行うかどうかのフラグ
bool	isTrigger	トリガーとしての衝突を行うかどうか

衝突イベントの処理方法

Unityでオブジェクト同士の衝突時に特別な処理をしたい場合は、特別なメッセージ関数を実装します。OnCollision### 関数がそれに該当します。

関数名	概要
OnCollisionEnter2D	衝突した瞬間に呼び出される
OnCollisionExit2D	衝突から離れた時に呼び出される
OnCollisionStay2D	衝突している最中に呼び出され続ける

このメッセージ関数を使って、衝突した瞬間を処理するスクリプトは以下のようになります。

衝突した瞬間をチェックする

void OnCollisionEnter2D(Collision2D coll) {
  // 何かのオブジェクトに衝突した
  if (coll.gameObject.tag == "Enemy") {
    // 敵と衝突したのでダメージ処理
    coll.gameObject.SendMessage("ApplyDamage", 10);
  }
}

isTrigger(トリガー)について

例えば、ゴールとなるゲートを通過した瞬間を判定したい場合、 OnClission### 系は衝突により反発する挙動を取るので使えません。そこで isTrigger を true にすることで、衝突の検知のみを行うようにすることができます。この場合はトリガー系関数( OnTrigger### )を使います。

関数名	概要
OnTriggerEnter2D	衝突した瞬間に呼び出される
OnTriggerExit2D	衝突から離れた時に呼び出される
OnTriggerStay2D	衝突している最中に呼び出され続ける

シューティングゲームなどでは、衝突を検知したらどちらかが消滅することが多いので、トリガー系を使うほうがよいです。
スクリプトでの実装例は以下のようになります。

トリガーを使った衝突判定

// 流砂に入り込んだかどうか
public bool characterInQuicksand;

void OnTriggerEnter2D(Collider2D other) {
  // 流砂に入った
  characterInQuicksand = true;
}

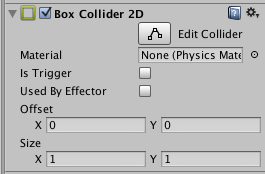
BoxCollider2D

2Dの矩形での衝突を判定するコンポーネントです。

型	変数名	概要	Inspector上での名称
Vector2	center	矩形の中心座標	-
Vector2	size	矩形の幅と高さ。中心からの幅と高さはこの半分の値となる	Size

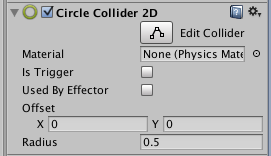
CircleCollider2D

2Dの円での衝突を判定するコンポーネントです。

型	変数名	概要	Inspector上での名称
Vector2	center	円の中心座標	-
float	radius	円の半径	Radius

クラス

2Dゲームを作るときによく使う、ベクトル・Mathf・GameObjectの説明をします。

クラス名	概要	リファレンス
Vector2D	2次元ベクトル	http://docs.unity3d.com/jp/current/ScriptReference/Vector2.html
Vector3D	3次元ベクトル	http://docs.unity3d.com/jp/current/ScriptReference/Vector3.html
Mathf	数学関数	http://docs.unity3d.com/jp/current/ScriptReference/Mathf.html
GameObject	ゲームオブジェクト	http://docs.unity3d.com/jp/current/ScriptReference/GameObject.html

Vector2 / Vector3

Vector2 / Vector3はベクトルで、x成分とy成分、z成分(Vector3のみ)を持っています。そして長さを求めたり、正規化することができます。

戻り値	関数名	概要
float	magnitude	ベクトルの長さを求める
Vector2	normalized	正規化した値を返す。現在のベクトルを正規化したい場合はNormalizeを使用する

Mathf

Mathfは数学関数を扱います。おなじみの Sin / Cos / Tan などの三角関数や、角度⇔ラジアンの変換、線形補間などの関数が用意されています。

分類	関数名(引数)	概要
符号	Abs(x)	絶対値を求める
符号	Sign(x)	xの符号を返す。xが負のときは-1を返し、正のときは1を返す
三角関数	Sin(x)	サインを求める
三角関数	Asin(x)	アークサインを求める
三角関数	Cos(x)	コサインを求める
三角関数	Acos(x)	アークコサインを求める
三角関数	Tan(x)	タンジェントを求める
三角関数	Atan(x)	アークタンジェントを求める
三角関数	Atan2(y,x)	アークタンジェントを求める
小数点	Ceil(x)	小数点を切り上げる
小数点	CeilToInt(x)	小数点を切り上げてIntで返す
小数点	FloorToInt(x)	小数点を切り捨ててIntで返す
小数点	Round(x)	小数点を四捨五入する
小数点	RoundToInt(x)	小数点を四捨五入してIntで返す
丸め処理	Clamp(val,min,max)	valをmin〜maxの間に値を丸める
丸め処理	Clamp01(x)	0.0〜1.0に値を丸める
角度	DeltaAngle(a,b)	bからaへの角度差を求める
補完	InverseLerp(from,to,t)	from〜toの値を逆補完する
補完	Lerp(from,to,t)	from〜toの値をt(0.0〜1.0)で補完する
補完	LerpAngle(from,to,t)	from〜toの値(0〜360に丸める)をt(0.0〜1.0)で角度補完する
補完	SmoothDamp(cur,tar,val,t,s,dt)	t秒かけてcurからtarに移動する値を求める
補完	SmoothDampAngle(cur,tar,val,t,s,dt)	SmoothDampの角度(0〜360)対応版
補完	SmoothStep(from,to,t)	from〜toの範囲をtで補完する
比較	Max(a,b)	aとbを比較して大きい方を返す
比較	Min(a,b)	aとbを比較して小さい方を返す
比較	Approximately(a, b)	Float同士を比較する。ほぼ一致してればtrueを返す
移動	MoveToward(current,target,maxDelta)	currentからtargetに向かってmaxDeltaの速さで移動する
移動	MoveTowardsAngle(current,target,maxDelta)	MoveTowardの角度(0〜360)対応版
移動	PingPong(t,length)	tを0〜lengthの範囲を往復するように移動する
移動	Repeat(t,length)	tを0〜legthの範囲を繰りかえす。整数値での剰余を求めるのと同じ
べき乗	Sqrt(x)	平方根を求める
べき乗	Pow(x,y)	xのy乗を求める
べき乗	IsPowerOfTwo(x)	xが2のべき乗の場合にtrueを返す
べき乗	ClosestPowerOfTwo(x)	xの値から最も近い2のn乗を返す
べき乗	NextPowerOfTwo(x)	xの値以上の最も近い2のn乗を返す
べき乗	Log(x,n)	底(n)に対するxの対数を求める
べき乗	Log10(x)	10を底とするxの対数を求める
べき乗	Exp(n)	自然対数eのn乗を返す
その他	PerlinNoise(x,y)	パーリンノイズを生成する
その他	LinearToGammaSpace(x)	線形からガンマのカラー空間へ値を変形する
その他	GammaToLinearSpace(x)	ガンマのカラー空間から線形へ値を変形する

サンプル

Mathfによる2Dのゲームでよく使いそうなサンプルをまとめてみました。

角度←→ラジアンの相互変換

シューティングゲームなどでは特定方向に弾を撃つ、という処理を行いますが、角度指定で発射できると便利です（例えば、175度・180度・185度に3wayショットを撃つなど）。

角度をラジアンに変換する

float deg = 40; // 40度
// 度をラジアンに変換
float rad = deg * Mathf.Deg2Rad;

ラジアンを度に変換する

float rad = 10.0f; // 10ラジアン
// ラジアンを度に変換
float deg = rad * Mathf.Rad2Deg;

絶対値を求める

絶対値を求める

float val;
if(Mathf.Abs(val) < 1) {
  // valが-1〜1であれば何か処理する
}

2つの角度差を求める

以下は、敵がいる方向に向かって旋回するサンプルコードです。

2つの角度差を求める

// 敵がいる方向に向かって旋回する
// 敵がいる方向
var a;
// 自分が向いている向き
var b = transform.eulerAngles.z;

// 角度差を求める
var d = Mathf.DeltaAngle(a, b);
// 旋回する
Vector3 v = new Vector3(0, 0, b + (d * 0.1f));
// 回転角度を反映
transform.eulerAngles = v;

線形補完

線形補完

// aからbへ線形補完する
float timer = 0.0f;
public Update() {
  float a = 0.0f;
  float b = 100.0f;

  timer += 0.01f;
  float d = Mathf.Lerp(a, b, timer);
}

GameObject

GameObjectは、Unity上でのすべてのオブジェクトのベースクラスとなります。何でも入る容器のようなものですが、これ単体では何もしません。コンポーネントを追加することで、必要な機能を追加することができます。また、ゲームオブジェクトのスクリプトから制御する場合、それが継承する Monobehavious が必要な機能をほとんど持っているため、このクラスを通して何か処理をすることはあまりありません。
ただ、Hierarchyビューにある他のゲームオブジェクトを取得する Find 系のstatic関数は便利なので、これだけは知っておいたほうがよいです。

戻り値	関数名(引数)	概要
GameObject	Find(name)	nameに指定したゲームオブジェクトを取得する。見つからない場合はnullを返す
GameObject	FindWithTag(tag)	tagに指定したタグを持つゲームオブジェクトを取得する。見つからない場合はnullを返す
GameObject[]	FindGameObjectsWithTag(tag)	tagに指定したタグを持つゲームオブジェクトのリストを取得する。見つからない場合はnullを返す

Find関数は、そのままゲームオブジェクト名を指定して取得できます。例えば"Enemy"というゲームオブジェクトが存在すれば、以下のように記述することで取得できます。

"Enemy"ゲームオブジェクトの取得

// "Enemy"ゲームオブジェクトの取得
GameObject obj = GameObject.Find("Enemy");

ただ、Find関数はすべてのゲームオブジェクトを操作するので重たい処理となります。そのため、シーンの起動時のみ取得してキャッシュする、などの工夫が必要となります。
もし、毎フレーム処理しなければならない場合には、FindWithTagを使うと高速に処理することができます。

"TagEnemy"というタグを持つゲームオブジェクトの取得

// "TagEnemy"というタグを持つゲームオブジェクトの取得
GameObject obj = GameObject.FindWithTag("TagEnemy");

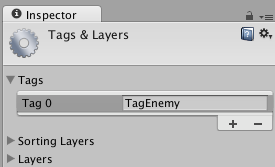
タグの登録は、メインメニューから Edit > Project Setting > Tags and Layers を選んで Tags から追加します。

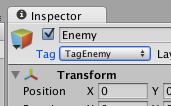
そして、対象となるゲームオブジェクトのInspectorビューから Tag のドロップダウンから設定します。

これで FindWithTag の検索対象となります。

GameObjectとMonoBehaviousの違いについて

Unityを始めたばかりの人が混乱しがちな、GameObjectとMonoBehaviousの違いについて補足します。
Unityではスクリプトから、ゲームオブジェクトが持つ要素にアクセスできるので、GameObjectとMonoBehaviousは同一のものであるかのように見えます。ですが実際には別モノです。

このように、ScriptはGameObjectが持つコンポーネントの一部にすぎません。
例えば、Enemyというゲームオブジェクトを作成し、Enemyというスクリプトをアタッチします。そしてEnemyスクリプトには以下のように記述します。

Enemy.cs

class Enemy : MonoBehavious
{
  // HP
  int _hp;

  // ダメージを与える
  public void Damage(int val)
  {
    _hp -= val;
  }
}

そして敵に攻撃が当たったので、敵にダメージを与えるとします。

HitAttack.cs

  // 攻撃が当たった
  Enemy e = (Enemy)GameObject.Find("Enemy");
  // 敵に100ダメージを与える
  e.Damage(100);

これは一見正しそうですが、型の変換に失敗してエラーとなります。EnemyはGameObjectではないからです。正しく処理するには以下のように記述します。

HitAttack.cs

  // 攻撃が当たった
  GameObject obj = GameObject.Find("Enemy");
  // Enemyスクリプトを取得
  Enemy e = obj.GetComponent<Enemy>();
  // 敵に100ダメージを与える
  e.Damage(100);

EnemyスクリプトはGameObjectが持つコンポーネントなので、GetComponentで取得する必要があります。